题目内容
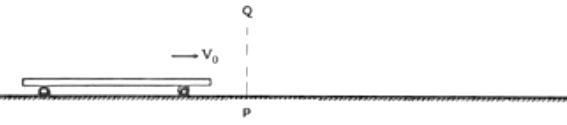
【题目】如图，水平面上有一条长直固定轨道，P为轨道上的一个标记点，竖直线PQ表示一个与长直轨道垂直的竖直平面，PQ的右边区域内可根据需要增加一个方向与轨道平行的水平匀强电场。在轨道上，一辆平板小车以速度v0=4m/s沿轨道从左向右匀速运动，当小车一半通过PQ平面时，一质量为m=1kg的绝缘金属小滑块（可视为质点）被轻放到小车的中点上，已知小滑块带电荷量为+2C且始终不变，滑块与小车上表面间的动摩擦因数为μ=0.2，整个过程中小车速度保持不变，g=10m/s2。求：
(1)若PQ右侧没有电场，木板足够长，在滑块与小车恰好共速时小滑块相对P点水平位移和摩擦力对小车做的功；
(2)当PQ右侧电场强度取
方向水平向右，且板长L=2m时，为保证小滑块不从车上掉下，则电场存在的时间满足什么条件？
（附加：若PQ右侧加一个向右的匀强电场，且木板长L=2m，为确保小滑块不从小车左端掉下来，电场强度大小应满足什么条件？）（此附加问为思考题，无需作答）
【答案】(1)4m，-16J；(2) 
；【附加】
【解析】
(1)小滑块放在小车上以后，其加速度根据牛顿第二定律
①
解得加速度
加速到共速时用时t1
②
解得
此过程中小滑块相对P点移动的距离
③
此过程中木板相对P点移动的距离
④
求解可得
摩擦力对小车做的功
⑤
求解可得
(2)当电场
时，小滑块相对运动到木板最左端后，会向右做匀加速运动，设时间为t3后撤去电场，之后滑块做减速运动，经时间t4，小滑块和小车在小车右端共速，恰好没掉下来，小滑块向右加速度为
⑩
解得
加速的末速度
减速过程中
加速过程中的位移为
减速过程中的位移为
则
联立⑩求解解得
所以电场存在总时间
所以电场存在的时间满足关系式（结果可以保留根式）
解法2：当电场时，小滑块相对运动到木板最左端后，会向右做匀加速运动，设时间为t3后撤去电场
小滑块向右加速度为
⑩
解得
滑块相对小车做加速度为
，初速度为零的匀加速运动，经时间t3后做加速度为
的匀减速运动直至相对静止，此过程中的总位移小于等于板长，因此
加速过程的时间
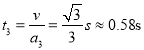
所以电场存在总时间
所以电场存在的时间满足关系式
附加问：当加有向右电场时，小滑块加速度
⑦
恰好运动到木板左端共速，共速时间
⑧
根据两物体的位移关系可得
⑨
联立⑦⑧⑨可得
所以电场强度E满足
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
