题目内容
11. 如图所示,直角坐标系xOy,X轴正方向沿着绝缘粗糙水平面向右,y轴正方向竖直向上.空间充满沿X轴负方向、E=2.0×104N/C的匀强电场.一个质量m=2.0×10-3kg、电量q=2.0×10-6C的带正电的物块(可作为质点),从O点开始以v0=10.0m/s的初速度沿着X轴正方向做直线运动,物块与水平面间动摩擦因数μ=0.5,g=10m/s2.
如图所示,直角坐标系xOy,X轴正方向沿着绝缘粗糙水平面向右,y轴正方向竖直向上.空间充满沿X轴负方向、E=2.0×104N/C的匀强电场.一个质量m=2.0×10-3kg、电量q=2.0×10-6C的带正电的物块(可作为质点),从O点开始以v0=10.0m/s的初速度沿着X轴正方向做直线运动,物块与水平面间动摩擦因数μ=0.5,g=10m/s2.(1)求带电物体在t=0.8s内通过的位移x
(2)若在0.8s末突然将匀强电场的方向变为沿y轴正方向,场强大小保持不变.求1.0s物体的坐标和在0〜1.0s内带电物体电势能的变化量△E.
分析 (1)带电物体在t=0.8s内,水平方向受到向左的滑动摩擦力和电场力,先向右做匀减速运动,根据牛顿第二定律得到加速度a1,由运动学公式求出匀减速到停下的时间和位移.之后物体向左做匀加速运动,由牛顿第二定律和运动学公式结合求出时间和位移,即可求出物体在t=0.8s内通过的位移x.
(2)0.8s内电场力做功为W1=-Eqx.0.8s后,带电物块受到竖直向上的电场力F=Eq=4.0×10-2N>mg,带电物块开始在水平方向做匀速运动,竖直方向做初速为零的匀加速运动,由牛顿第二定律和运动学公式结合求出竖直方向的位移y,电场力对带电物块做功为W2=Eqy,则0~1.0s内电场力对带电物块所做的总功为W=W1+W2
解答 解:(1)设带电物块向右做匀减速直线运动过程中,加速度大小为a1,时间为t1,通过的位移为x1,则
Eq+μmg=ma1
又t1=$\frac{{v}_{o}}{{a}_{1}}$
x1=$\frac{{v}_{0}^{2}}{2{a}_{1}}$
解得:a1=25 m/s2,t1=0.4 s,x1=2 m
t1=0.4 s之后,带电物块向左做匀加速直线运动,设加速度大小为a2,时间为t2,通过的位移为x2,则有:
Eq-μmg=ma2
t2=t-t1
x2=$\frac{1}{2}$a2t22=1.2m
解得:a2=15m/s2,t2=0.4 s,x2=1.2m
x=x1-x2=0.8m,方向水平向右.
(2)设0.8s内电场力做功为W 1,则有:W1=-Eqx=-3.2×10-2J
0.8s后,设带电物块受到竖直向上的电场力为F,且F=Eq=4.0×10-2N>mg,所以,带电物块开始在水平方向做的匀速运动,竖直方向做初速为零的匀加速运动,设加速度为a3,在竖直方向的位移为y,电场力做功为W 2,
则F-mg=ma3
解得:a3=10m/s2,
t3=1.0-t1=0.2s
则得:y=$\frac{1}{2}$a3t32=0.2m
W2=Eqy=8.0×10-3J
设0~1.0s内电场力对带电物块所做的总功为W,则有:W=W1+W2=-2.4×10-2J
即:△E=-W=2.4×10-2J
答:(1)求带电物体在t=0.8s内通过的位移x是0.8m,方向水平向右.
(2)在0〜1.0s内带电物体电势能的变化量△E是2.4×10-2J
点评 本题是多过程问题,关键是理清物体在整个过程中的运动情况,结合牛顿第二定律及运动学公式进行求解

| A. | 只要是小的物体就可看做质点 | |
| B. | 只要是做直线运动的物体就可看做质点 | |
| C. | 做曲线运动的物体都不能看做质点 | |
| D. | 在平直公路上行驶的汽车,当把汽车作为一个整体来研究它的运动时,可把汽车看做质点 |
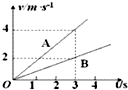 如图所示为两个物体A和B在同一直线上沿同一方向同时做匀加速运动的v-t图线.已知在第3s末两个物体在途中相遇,则下列说法正确的是( )
如图所示为两个物体A和B在同一直线上沿同一方向同时做匀加速运动的v-t图线.已知在第3s末两个物体在途中相遇,则下列说法正确的是( )| A. | 3s内两物体的位移相等 | B. | 第3s末两物体速度相等 | ||
| C. | 第3s末两物体的加速度相等 | D. | B的出发点在A的出发点前3m处 |
| A. | 氡的半衰期为3.8天,若取100个氡原子核,经7.6天后就一定剩下25个原子核了 | |
| B. | 重核裂变会释放出核能,产生的中等质量的核的比结合能大于原来重核的比结合能 | |
| C. | 光子的波长越长,则光子的能量就越大 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,电势能增大,原子的总能量增大 |
| A. | △v=0 W=0 | B. | △v=12m/s W=0 | ||
| C. | △v=12m/s W=10.8J | D. | △v=0 W=10.8J |
 如图所示,是某质点运动的v-t图象,请回答:
如图所示,是某质点运动的v-t图象,请回答: 如图所示,放在长木板上的木块质量为1Kg,当木板与水平方向夹角为30°时,木块静止在长木板上.
如图所示,放在长木板上的木块质量为1Kg,当木板与水平方向夹角为30°时,木块静止在长木板上.