题目内容
【题目】如图所示,在光滑的圆锥顶用长为L的轻质细线悬挂一可视为质点的质量为m的小球。圆锥体轴线AB沿竖直方向,母线与轴线之间的夹角为θ=37,若物体跟随圆锥体且绕轴线AB做水平面内的圆周运动,已知重力加速度为g。sinOθ=0.6,cosθ=0.8,求:
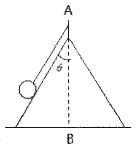
(1)当![]() 时,求线对物体的拉力大小;
时,求线对物体的拉力大小;
(2)当![]() 时,求线对物体的拉力大小。
时,求线对物体的拉力大小。
【答案】(1) 1.05mg (2) 2mg
【解析】试题分析:先求出小球刚要离开锥面时的临界速度,此时支持力为零,根据牛顿第二定律求出该临界速度.当速度大于临界速度,则物体离开锥面,当速度小于临界速度,物体还受到支持力,根据牛顿第二定律,物体在竖直方向上的合力为零,水平方向上的合力提供向心力,求出绳子的拉力。
当小球刚要离开锥面时的临界条件为圆锥体对小球的支持力![]() ,
,
由牛顿第二定律得: ![]()
解得: ![]()
(1)因为![]() ,
, ![]() ,对小球受力分析如图1所示:
,对小球受力分析如图1所示:
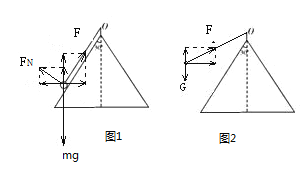
则得: ![]()
![]()
解得:F=1.05mg.
(2)当![]() ,物体离开斜面对小球受力分析如图2所示,则有:
,物体离开斜面对小球受力分析如图2所示,则有:
Fcosα-mg=0
![]()
解得:F=2mg

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目