题目内容
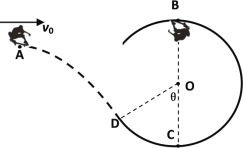
【题目】如图所示小球A用长为L的细线悬挂与O点,且与水平面刚好接触,另一相同的小球B从固定的光滑曲面h高处由静止下滑,然后沿水平面向右运动S距离后与A球发生对心碰撞。设曲面底端与水平面平滑连接,且mA=mB,A、B两球碰撞时无机械能损失。求

(1)若水平面光滑,且h=3L,试通过计算说明A、B两球碰撞后各如何运动?
(2)若水平面不光滑,且B球在水平面上滑动时与水平面间的动摩擦因数μ=0.2,h=L=1 m,S=0.5 m,则A、B两球共发生多少次碰撞?B球最终停在何处?
【答案】(1)B与A碰后,B停止,A做圆周运动,经一周后,A再次与B相碰,A停止,B向右以![]() 的速度做匀速直线运动(2)最后一定停在曲面的低端。每经过一次往复,碰撞两次,所以共碰撞10次
的速度做匀速直线运动(2)最后一定停在曲面的低端。每经过一次往复,碰撞两次,所以共碰撞10次
【解析】
(1)设A与B碰前B的速度为![]() ,B沿曲面下滑时由机械能守恒得mBgh=
,B沿曲面下滑时由机械能守恒得mBgh=![]() ,得
,得![]() =
=![]()
A、B碰撞动量守恒有:mBvB=mAvA+mBvB
A、B碰撞能量守恒有:![]() mBvB2+
mBvB2+![]() mAvA2=
mAvA2=![]() mBvB2+
mBvB2+![]() mAvA2
mAvA2
因mA=mB,得碰后方B、A的速度分别为:vB=0,vA=![]()
设A到最高点的速度为vc,A做圆周运动在最高点的临界条件为:mAg=mA![]()
A作圆周运动时机械能守恒有:![]() mAvA2=
mAvA2=![]() mAvC2+mAg
mAvC2+mAg![]() 2L
2L
代入vA=![]() 得h=2.5L<3L
得h=2.5L<3L
故B与A碰后,B停止,A做圆周运动,经一周后,A再次与B相碰,A停止,B向右以![]() 的速度做匀速直线运动。
的速度做匀速直线运动。
(2)因L=h且水平面粗糙,故A、B第一次碰后,A上摆高度必小于L,到达最高点后又左摆动与B球相碰交换速度,B球向左运动达曲面上某高度下滑,沿水平面向右运动,与球发生第二次碰撞,如此反复。设B球在水平面上运动的总路程为x,由能的转化和守恒定律得:
![]() mBgx=mBgh,x=
mBgx=mBgh,x=![]() =
=![]() =5m=10S,因为小球B在水平面上每经过一次往复与A球碰撞两次,所以共碰撞10次,最后一定停在曲面的底端。
=5m=10S,因为小球B在水平面上每经过一次往复与A球碰撞两次,所以共碰撞10次,最后一定停在曲面的底端。