题目内容
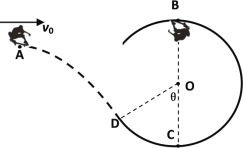
【题目】如图所示,一个质量为60 kg滑板运动员,以v 0=4![]() m/s初速度从某一高台的A点水平飞出,恰好从光滑竖直圆轨道的D点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=3 m,θ=60°,取g=10 m/s2,求:
m/s初速度从某一高台的A点水平飞出,恰好从光滑竖直圆轨道的D点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=3 m,θ=60°,取g=10 m/s2,求:
(1)滑板运动员在空中的飞行时间。
(2)滑板运动员运动到圆弧轨道最高点B时轨道对他的作用力。
【答案】(1)t=1.2s (2)FN=1440N,方向向下
【解析】
(1)设运动员到D点时竖直分速度为vy,tan300=![]() ,解得vy=12m/s,由于vy=gt可得滑板运动员在空中的飞行时间t=1.2s
,解得vy=12m/s,由于vy=gt可得滑板运动员在空中的飞行时间t=1.2s
(2)设运动员到达D点时速度为![]() ,到达B点时速度为
,到达B点时速度为![]() ,D点到圆心的竖直高度为h
,D点到圆心的竖直高度为h
![]() =
=![]() ,h=Rcos600=0.5R,由机械能守恒可得:
,h=Rcos600=0.5R,由机械能守恒可得:![]() m
m![]() +mg(R+h)=
+mg(R+h)=![]() m
m![]() ,解得
,解得![]() =102m2/
=102m2/![]() ,由于物体通过圆周运动的最高点应满足v=
,由于物体通过圆周运动的最高点应满足v=![]() ,即v2=gR=30m2/
,即v2=gR=30m2/![]() ,因为
,因为![]() =102m2/
=102m2/![]() gR,所以滑板运动员能顺利通过最高点。
gR,所以滑板运动员能顺利通过最高点。
设运动员在最高点时轨道对他的作用力为FN,根据牛顿第二定律有:mg+FN=m![]()
解得滑板运动员运动到圆弧轨道最高点B时轨道对他的作用力:FN=1440N,方向向下

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目