题目内容
【题目】如图所示，竖直平面内的直角坐标系xOy把空间分成四个区域，一绝缘带孔弹性挡板放置在x轴，某一端与坐标系O点重合，挡板上的小孔M距0点距离L1=9m，在y轴上的N点有一开口的小盒子，小盒子的中心距O点的距离L2=3m，空间中I、Ⅲ、Ⅳ象限存在竖直向上的匀强电场．小孔M正上方高为h处有一直径略小于小孔宽度的带正电小球（视为质点），其质量m=1.0×10﹣3kg，电荷量q=1.0×10﹣3C，若h=0.8m，某时刻释放带电小球．经t=0.55s小球到达小孔正下方L3=0.6m的S点（S未画出），不计空气阻力，g=10m/s2，sin37°=0.6，cos37°=0.8．
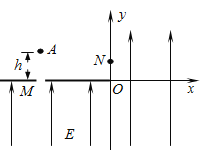
（1）求小球运动到小孔M时速度的大小；
（2）求电场强度E的大小；
（3）若在空间中Ⅰ、Ⅲ、Ⅳ象限再加一垂直纸面的匀强磁场，B=1T，适当改变h为合适的一些数值，其他条件不变，小球仍由静止释放，小球通过小孔后继续运动，小球与挡板相碰以原速度反弹，碰撞时间不计，碰撞电量不变，如果小球最后都能落入盒子的中心处，求h的可能值．
【答案】（1）
（2）
（3）1.25m，0.45m，0.70m．
【解析】(1) 小球释放做自由落体运动有 
， 
，解得 t1=0.4s，v=4m/s；
(2) 小球进入电场后在重力和电场力作用下做直线运动，设加速度为a，根据题意有
，其中t2=t-t1=0.15s，解得a=0，表明小球进入电场后做匀速直线运动
故有 qE=mg，解得 E=10 V/m；
(3) 加上匀强磁场后，小球进入复合场做匀速圆周运动，小球进入复合场的速度垂直挡板，做圆周运动的圆心必在x轴上，如果与挡板相碰，其轨迹前面部分是半圆，且圆的半径
R≥3m（因L2=3m），R越小，小球碰撞次数越多．设经n次碰撞后小球达到N点；
所以 n·2R≤L1，即n·2R≤9，解得 n≤1.5，即取n= 0，1
所以小球从小孔到盒子中心的运动轨迹可能有下列三种情况：
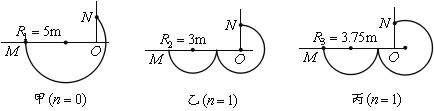
由几何知识得：
甲图 
，代入数据解得R1=5m；
乙图 3R2=L1， 代入数据解得R2=3m；
丙图 
，代入数据解得R3=3.75m；
根据 
分别代入上述数据解得 h1=1.25m，h2=0.45m，h3=0.70m
