题目内容
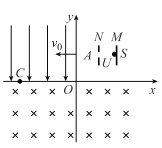
【题目】如图所示，间距为L的光滑金属导导轨MNP和M′N′P′由圆弧和水平两部分组成，圆弧和水平部分光滑连接，在水平导轨NPP′N′间存在磁感强度为B的匀强磁场，磁场垂直导轨平面向上，在M和M′之间连接一个电阻为R的定值电阻。现在将一根与导轨垂直、质量为m、电阻为2R的金属杆ab从圆弧轨道上距水平面高度为h处释放，金属棒恰能到达PP′处。导轨电阻不计，重力加速度为g。
（1）金属棒刚进入磁场时的加速度；
（2）水平导轨NP的长度s；
（3）若在PP′处安装有一储能装置，每次释放相同的能量，将恰好到达PP′处的金属棒弹回，使得金属棒可以在导轨上做周期性的运动，试求每个周期里定值电阻R中产生的焦耳热Q。
[Failed to download image : http://192.168.0.10:8086/QBM/2020/7/14/2505524454219776/2505593607577600/STEM/275c04a7819848db8a8c38fe97409390.png]
【答案】（1）
，方向水平向左；（2）
；（3）
【解析】
（1）金属棒从静止开始下滑到水平面过程中，根据机械能守恒，则有
则感应电动势为
感应电流为
根据牛顿第二定律有
联立解得
根据右手定则可知，电流方向由a到b，故根据左手定则可知，安培力方向水平向左，所以加速度方向也是水平向左。
（2）金属棒从进入磁场到
处停下，根据动量定理有
代入
，可得
变形得
两边求和，可得
解得
（3）整个过程，根据动量定理可得
解得
直接滑下时
返回时
故每个周期里定值电阻R中产生的焦耳热
练习册系列答案
相关题目
