题目内容
【题目】如图所示,在倾角为37°的足够长的光滑斜面上,放一质量为 mA=0.2kg的薄板A, A板上、下段由不同材料构成,下段表面光滑,长度 l=3m,上段表面粗糙;质量为 mB=2.0kg 的金属块 B(视为质点)位于A的最下端,B与 A上段间的动摩擦因数μ=0.1;质量为 mC=1.2kg 的物块 C通过轻线绕过定滑轮与 B相连。忽略滑轮质量及轴间的摩擦,A、B间最大静摩擦力可认为等于滑动摩擦力。开始时,整个系统在外力作用下,处于静止状态,轻线被拉直。(sin370=0.6, cos370=0.8,g=10m/ s2。)求:
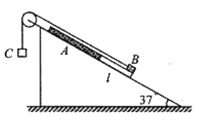
(1)撤去外力的瞬间,A、 B、 C的加速度分别是多大;
(2)B刚到达A的粗糙部分时,A、 B、 C的加速度分别是多大;
(3)撤去外力后的整个过程中,因摩擦产生的热量Q,绳足够长,B始终没滑出A板
【答案】(1)![]() (2)
(2)![]() (3)11.52J
(3)11.52J
【解析】
(1)由于mBgsin37°=mcg=12N 所以,撤去外力的瞬间aB=ac=0
对薄板A,有mAgsin37°=mAaA
得aA=6m/s2
(2)由于斜面和A板下段表面都光滑,撤去外力后,A板从静止开始向下做匀加速运动,只要金属块B在A板下段表面上,B、C就保持静止不动.A板运动到金属块B在其上段表面上后,B和C受滑动摩擦力作用将一起以相同大小的加速度做加速运动.设A板上段刚滑到B下方时速度为vA,则vA2=2aAl
解得vA=6m/s
B在A板上端表面时,设A板加速度为aA1,B和C加速度为aB1,轻线拉力为F,则
mAgsin37°-μmBgcos37°=mAaA
mBgsin37°+μmBgcos37°-F=mBaB1
F-mCg=mCaB1
解得aA1=-2m/s2,aB1 =aC1=0.5m/s2
(3)A、B、C最终达到速度相等.假设速度相等之后,A、B间的静摩擦力f小于最大静摩擦力fm,即A、B相对静止,A、B、C三者加速度大小相同,设为a0,则
(mA+mB)gsin37°-mCg=(mA+mB+mC)a0
mAgsin37°-f=mAa0
a0=0.5m/s2,f=1.1N
fm=μmBgcos37°=1.6N
即f<fm,假设成立,之后A、B相对静止.
设A、B、C达到相等速度v1所需时间为t,则
v1=vA+aA1t=aB1t
解得t=2.4s,v1=1.2m/s
设在时间t内,A通过的距离是xA,B和C通过的距离是xB,则
xA=![]() (vA+v1)t
(vA+v1)t
xB=![]() v1t
v1t
解得xA=8.64m,xB=1.44m
Q=μmBg(xA-xB)cos37°
Q=11.52J