题目内容
【题目】如图所示，速度选择器两板间电压为U、相距为d，板间有垂直纸面向里、磁感应强度为B0的匀强磁场；在紧靠速度选择器右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，磁感应强度B未知，圆形磁场区域半径为R。一质量为m、电荷量为q的带正电的粒子在速度选择器中做直线运动，从M点沿圆形磁场半径方向进入磁场，然后从N点射出，O为圆心，∠MON＝120°，粒子重力可忽略不计。求：
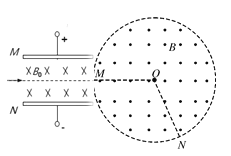
(1)粒子在速度选择器中运动的速度大小；
(2)圆形磁场区域的磁感应强度B的大小；
(3)粒子在圆形磁场区域的运动时间。
【答案】（1）
（2）
（3）
【解析】试题分析：粒子进入平行金属板做匀速直线运动，粒子所受的电场力和洛伦兹力平衡，由平衡条件可求出速度大小v；离子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，画出轨迹，由几何知识求出轨迹半径，根据牛顿第二定律求出圆形磁场区域的磁感应强度B的大小；根据粒子在磁场中运动周期公式和圆心角即可求出粒子在圆形磁场区域的运动时间。
（1）粒子在速度选择器中做直线运动，由力的平衡条件得
解得： 
（2）粒子在磁场中做匀速圆周运动，轨迹如图所示：
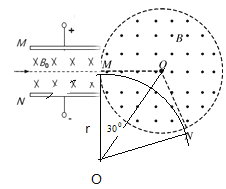
设其半径为r，由向心力公式得： 
由几何关系得： 
联立解得：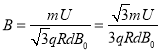 
（3）粒子在磁场中运动周期为： 
根据几何关系可知粒子在磁场中的圆心角为600，；联立以上可得运动时间为： 
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
