题目内容
1.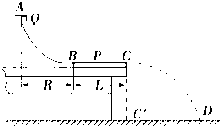 有同学设计用如图所示的实验装置测量小物块Q与平板P之间的动摩擦因数μ.光滑的$\frac{1}{4}$圆弧轨道AB在B点与水平固定的平板P上表面BC相切,C点在水平地面的垂直投影为C′,重力加速度大小为g.实验步骤如下:
有同学设计用如图所示的实验装置测量小物块Q与平板P之间的动摩擦因数μ.光滑的$\frac{1}{4}$圆弧轨道AB在B点与水平固定的平板P上表面BC相切,C点在水平地面的垂直投影为C′,重力加速度大小为g.实验步骤如下:①用天平称出物块Q的质量m;
②测出轨道AB的半径R、BC的长度L和CC′的高度h;
③将物块Q从A点静止释放,用复写纸在物块Q的落地处记录落地点;
④重复步骤③,共做10次;
⑤用圆规画一个尽量小的圆将10个落地点围住;
⑥测出圆心D到C′的距离s.
回答下列问题:
(1)步骤④⑤的目的是减小实验的偶然误差.
(2)物块Q与平板P间的动摩擦因数μ=$\frac{R}{L}$-$\frac{{s}^{2}}{4hL}$.(用上述测量量表示)
(3)结果发现实验测得的μ值总是比实际值偏大(可见是系统误差),请找出造成该系统误差的可能来源圆弧轨道与滑块间有摩擦(写出一个即可).
分析 (1)多次实验的目的是减小实验误差;
(2)物块由A到B点过程,由动能定理可以求出物块到达B时的动能;物块离开C点后做平抛运动,由平抛运动的知识可以求出物块在C点的速度,然后求出在C点的动能;由B到C,由动能定理可以求出克服摩擦力所做的功;由功的计算公式可以求出动摩擦因数.
(3)误差偏大的原因是存在摩擦阻力.
解答 解:(1)实验步骤④⑤的目的,是通过多次实验减小实验结果的偶然误差;
(2)从A到B,由动能定理得:mgR=EKB-0,则物块到达B时的动能:EKB=mgR;
离开C后,物块做平抛运动,
水平方向:s=vCt,
竖直方向:h=$\frac{1}{2}$gt2,
物块在C点的动能:EKC=$\frac{1}{2}$mvC2,
解得:EKC=$\frac{mg{s}^{2}}{4h}$;
由B到C过程中,由动能定理得:
-Wf=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvB2,
克服摩擦力做的功:Wf=mgR-$\frac{mg{s}^{2}}{4h}$;
B到C过程中,克服摩擦力做的功:
Wf=μmgL=mgR-$\frac{mg{s}^{2}}{4h}$,
则:μ=$\frac{R}{L}$-$\frac{{s}^{2}}{4hL}$;
(3)实验测得的μ值比实际值偏大,其原因除了实验中测量量的误差之外,其他的可能是圆弧轨道存在摩擦,接缝B处不平滑等.
故答案为:(1)减小实验的偶然误差;(2)$\frac{R}{L}-\frac{s^2}{4hL}$;(3)圆弧轨道与滑块间有摩擦.
点评 熟练应用动能定理、平抛运动规律、功的计算公式即可正确解题,学会根据实验数据来实验结果分析,注意实验误差不会没有,只能降低.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9. 边长为L的正方形金属框abcd置于光滑水平面上,线框分别以v1、v2的速度匀速进入匀强磁场,线圈平面始终保持与磁场垂直.已知v1:v2=1:2,则两次进入磁场的过程中( )
边长为L的正方形金属框abcd置于光滑水平面上,线框分别以v1、v2的速度匀速进入匀强磁场,线圈平面始终保持与磁场垂直.已知v1:v2=1:2,则两次进入磁场的过程中( )
 边长为L的正方形金属框abcd置于光滑水平面上,线框分别以v1、v2的速度匀速进入匀强磁场,线圈平面始终保持与磁场垂直.已知v1:v2=1:2,则两次进入磁场的过程中( )
边长为L的正方形金属框abcd置于光滑水平面上,线框分别以v1、v2的速度匀速进入匀强磁场,线圈平面始终保持与磁场垂直.已知v1:v2=1:2,则两次进入磁场的过程中( )| A. | 线圈中感应电流方向为adcba | B. | 通过线圈的电流之比为1:2 | ||
| C. | 线圈所受水平外力之比为1:1 | D. | 线圈内产生的电热之比为1:4 |
6.完全相同的三块木块并排固定在水平面上,一颗子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,且穿过第三块木块后速度恰好为零,则子弹依次射入每块木块时的速度之比和穿过每块木块所用时间之比为( )
| A. | v1:v2:v2=1:2:3 | B. | ${v_1}:{v_2}:{v_2}=\sqrt{3}:\sqrt{2}:1$ | ||
| C. | ${t_1}:{t_2}:{t_2}=1:({\sqrt{2}-1}):({\sqrt{3}-\sqrt{2}})$ | D. | ${t_1}:{t_2}:{t_2}=({\sqrt{3}-\sqrt{2}}):({\sqrt{2}-1}):1$ |
13.一遥控玩具汽车在平直路面上运动的位移-时间图象如图所示,则下列说法中错误的是( )


| A. | 前15s内汽车的位移为300m | B. | 前10s内汽车的加速度为零 | ||
| C. | 10s--15s内汽车处于静止状态 | D. | 15s--25s内汽车做匀减速直线运动 |
11.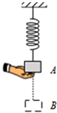 如图所示,轻质弹簧上端固定,下端系一物体.物体在A处时,弹簧处于原长状态.现用手托住物体使它从A处缓慢下降,到达B处时,手和物体自然分开.此过程中,物体克服手的支持力所做的功为W.不考虑空气阻力.关于此过程,下列说法正确的有( )
如图所示,轻质弹簧上端固定,下端系一物体.物体在A处时,弹簧处于原长状态.现用手托住物体使它从A处缓慢下降,到达B处时,手和物体自然分开.此过程中,物体克服手的支持力所做的功为W.不考虑空气阻力.关于此过程,下列说法正确的有( )
 如图所示,轻质弹簧上端固定,下端系一物体.物体在A处时,弹簧处于原长状态.现用手托住物体使它从A处缓慢下降,到达B处时,手和物体自然分开.此过程中,物体克服手的支持力所做的功为W.不考虑空气阻力.关于此过程,下列说法正确的有( )
如图所示,轻质弹簧上端固定,下端系一物体.物体在A处时,弹簧处于原长状态.现用手托住物体使它从A处缓慢下降,到达B处时,手和物体自然分开.此过程中,物体克服手的支持力所做的功为W.不考虑空气阻力.关于此过程,下列说法正确的有( )| A. | 物体重力势能减小量小于W | |
| B. | 弹簧弹性势能增加量小于W | |
| C. | 物体与弹簧组成的系统机械能减少W | |
| D. | 若将物体从A处由静止释放,则物体到达B处时的动能为W |
 现要测量某小量程电流表的内阻,其内阻在15~18Ω之间,可选用的器材如下:
现要测量某小量程电流表的内阻,其内阻在15~18Ω之间,可选用的器材如下: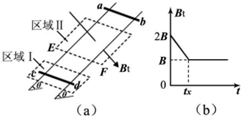 如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上,在区域Ⅰ内有方向垂直于斜面的匀强磁场,磁感应强度为B,在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域Ⅰ内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知ab棒和cd棒的质量为m、电阻为R,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰进入区域Ⅱ,重力加速度为g.求:
如图(a)所示,间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上,在区域Ⅰ内有方向垂直于斜面的匀强磁场,磁感应强度为B,在区域Ⅱ内有垂直于斜面向下的匀强磁场,其磁感应强度Bt的大小随时间t变化的规律如图(b)所示.t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑,同时下端的另一金属细棒cd在位于区域Ⅰ内的导轨上由静止释放.在ab棒运动到区域Ⅱ的下边界EF处之前,cd棒始终静止不动,两棒均与导轨接触良好.已知ab棒和cd棒的质量为m、电阻为R,区域Ⅱ沿斜面的长度为2L,在t=tx时刻(tx未知)ab棒恰进入区域Ⅱ,重力加速度为g.求: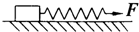 如图所示,轻质弹簧的劲度系数k=15N/cm,用其拉着一个重为300N的物体在水平面上运动,当弹簧的伸长量为4cm时,物体恰在水平面上做匀速直线运动,求:
如图所示,轻质弹簧的劲度系数k=15N/cm,用其拉着一个重为300N的物体在水平面上运动,当弹簧的伸长量为4cm时,物体恰在水平面上做匀速直线运动,求: