题目内容
6.完全相同的三块木块并排固定在水平面上,一颗子弹以速度v水平射入,若子弹在木块中做匀减速直线运动,且穿过第三块木块后速度恰好为零,则子弹依次射入每块木块时的速度之比和穿过每块木块所用时间之比为( )| A. | v1:v2:v2=1:2:3 | B. | ${v_1}:{v_2}:{v_2}=\sqrt{3}:\sqrt{2}:1$ | ||
| C. | ${t_1}:{t_2}:{t_2}=1:({\sqrt{2}-1}):({\sqrt{3}-\sqrt{2}})$ | D. | ${t_1}:{t_2}:{t_2}=({\sqrt{3}-\sqrt{2}}):({\sqrt{2}-1}):1$ |
分析 子弹依次射入每块木块做匀减速直线运动到零,采取逆向思维,子弹做初速度为零的匀加速直线运动,根据v2=2ax求出子弹依次射入每块木块的速度比;初速度为0的匀加速直线运动,在通过相等位移内的时间比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})$…根据该推论得出穿过每块木块所用的时间比.
解答 解:A、采取逆向思维,子弹做初速度为0的匀加速直线运动,有${{v}_{1}}^{2}=6ad$,${{v}_{2}}^{2}=4ad$,${{v}_{3}}^{2}=2ad$,所以${v}_{1}:{v}_{2}:{v}_{3}=\sqrt{3}:\sqrt{2}:1$.故A错误,B正确.
C、初速度为0的匀加速直线运动中,在通过相等位移内所用的时间比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})$…,则穿过每块木块所用时间之比为t1:t2:t3=$(\sqrt{3}-\sqrt{2})$:($\sqrt{2}$-1):1.故C错误,D正确.
故选:BD.
点评 本题采取逆向思维来做比较方便,解决本题的关键掌握初速度为0的匀加速直线运动中,在通过相等位移内所用的时间比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})$…

练习册系列答案
相关题目
14. 如图所示,DA、DB和CA是竖直平面内三根固定的光滑细杆,O为竖直平面内圆周的圆心,A、B、C、D位于同一圆周上,C为圆周的最高点,A为最低点,BD和AC都经过圆心O.现在每根杆上都套一个小滑环,分别从C点或D点无初速度释放,用t1表示滑环从D到达A所用的时间,用t2表示滑环从C到达A所用的时间,用t3表示滑环从D到达B所用的时间,则下列关系正确的是( )
如图所示,DA、DB和CA是竖直平面内三根固定的光滑细杆,O为竖直平面内圆周的圆心,A、B、C、D位于同一圆周上,C为圆周的最高点,A为最低点,BD和AC都经过圆心O.现在每根杆上都套一个小滑环,分别从C点或D点无初速度释放,用t1表示滑环从D到达A所用的时间,用t2表示滑环从C到达A所用的时间,用t3表示滑环从D到达B所用的时间,则下列关系正确的是( )
 如图所示,DA、DB和CA是竖直平面内三根固定的光滑细杆,O为竖直平面内圆周的圆心,A、B、C、D位于同一圆周上,C为圆周的最高点,A为最低点,BD和AC都经过圆心O.现在每根杆上都套一个小滑环,分别从C点或D点无初速度释放,用t1表示滑环从D到达A所用的时间,用t2表示滑环从C到达A所用的时间,用t3表示滑环从D到达B所用的时间,则下列关系正确的是( )
如图所示,DA、DB和CA是竖直平面内三根固定的光滑细杆,O为竖直平面内圆周的圆心,A、B、C、D位于同一圆周上,C为圆周的最高点,A为最低点,BD和AC都经过圆心O.现在每根杆上都套一个小滑环,分别从C点或D点无初速度释放,用t1表示滑环从D到达A所用的时间,用t2表示滑环从C到达A所用的时间,用t3表示滑环从D到达B所用的时间,则下列关系正确的是( )| A. | t1=t2=t3 | B. | t1=t2<t3 | C. | t1=t3<t2 | D. | t1<t2<t3 |
11. 如图所示,a,b,c为电场中同一条电场线(直线)上的三点,c为ab中点.a、b电势分别为ϕa=5V,ϕb=3V,下列叙述正确的是( )
如图所示,a,b,c为电场中同一条电场线(直线)上的三点,c为ab中点.a、b电势分别为ϕa=5V,ϕb=3V,下列叙述正确的是( )
 如图所示,a,b,c为电场中同一条电场线(直线)上的三点,c为ab中点.a、b电势分别为ϕa=5V,ϕb=3V,下列叙述正确的是( )
如图所示,a,b,c为电场中同一条电场线(直线)上的三点,c为ab中点.a、b电势分别为ϕa=5V,ϕb=3V,下列叙述正确的是( )| A. | 该电场在c点处的电势一定为4V | |
| B. | a点处的场强Ea一定大于b点处的场强Eb | |
| C. | 一正电荷在a点受到的电场力由a指向b | |
| D. | 一负电荷从a点运动到b点电场力做正功 |
18.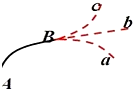 如图,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受力反向(大小不变),则物体以后的运动情况( )
如图,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受力反向(大小不变),则物体以后的运动情况( )
 如图,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受力反向(大小不变),则物体以后的运动情况( )
如图,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受力反向(大小不变),则物体以后的运动情况( )| A. | 可能沿曲线 Ba运动 | B. | 可能沿直线 Bb 运动 | ||
| C. | 可能沿曲线 Bc运动 | D. | 可能沿原曲线由 B 返回 A |
15.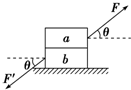 质量均为m的a、b两木块叠放在水平面上,如图所示,a受到斜向上与水平面成θ角的力F作用,b受到斜向下与水平面成θ角等大的力F′作用,两力在同一竖直平面内,此时两木块保持静止,下列说法正确的是( )
质量均为m的a、b两木块叠放在水平面上,如图所示,a受到斜向上与水平面成θ角的力F作用,b受到斜向下与水平面成θ角等大的力F′作用,两力在同一竖直平面内,此时两木块保持静止,下列说法正确的是( )
 质量均为m的a、b两木块叠放在水平面上,如图所示,a受到斜向上与水平面成θ角的力F作用,b受到斜向下与水平面成θ角等大的力F′作用,两力在同一竖直平面内,此时两木块保持静止,下列说法正确的是( )
质量均为m的a、b两木块叠放在水平面上,如图所示,a受到斜向上与水平面成θ角的力F作用,b受到斜向下与水平面成θ角等大的力F′作用,两力在同一竖直平面内,此时两木块保持静止,下列说法正确的是( )| A. | b对a的支持力一定等于mg | B. | 水平面对b的支持力一定等于2mg | ||
| C. | a、b之间一定存在静摩擦力 | D. | b与水平面之间可能存在静摩擦力 |
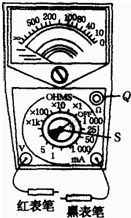 如图所示为一可供使用的多用电表,S为选择开关,Q为电阻挡调零旋钮.现在要用它检测电阻的阻值(图中未画电阻).已知大约阻值为R1=60Ω,下面提出了在测量过程中一系列可能的操作,请你选出能尽可能准确地测定各阻值和符合多用电表安全使用规则的各项操作,并且将它们按合理顺序填写在后面的横线上.
如图所示为一可供使用的多用电表,S为选择开关,Q为电阻挡调零旋钮.现在要用它检测电阻的阻值(图中未画电阻).已知大约阻值为R1=60Ω,下面提出了在测量过程中一系列可能的操作,请你选出能尽可能准确地测定各阻值和符合多用电表安全使用规则的各项操作,并且将它们按合理顺序填写在后面的横线上.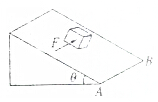 如图所示,在倾角θ=30°的斜面上放着一滑块,重为G,现用与AB边平行的水平推力F=$\frac{G}{2}$推滑块,恰能使滑块在斜面上做匀速直线运动.
如图所示,在倾角θ=30°的斜面上放着一滑块,重为G,现用与AB边平行的水平推力F=$\frac{G}{2}$推滑块,恰能使滑块在斜面上做匀速直线运动.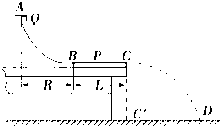 有同学设计用如图所示的实验装置测量小物块Q与平板P之间的动摩擦因数μ.光滑的$\frac{1}{4}$圆弧轨道AB在B点与水平固定的平板P上表面BC相切,C点在水平地面的垂直投影为C′,重力加速度大小为g.实验步骤如下:
有同学设计用如图所示的实验装置测量小物块Q与平板P之间的动摩擦因数μ.光滑的$\frac{1}{4}$圆弧轨道AB在B点与水平固定的平板P上表面BC相切,C点在水平地面的垂直投影为C′,重力加速度大小为g.实验步骤如下: