题目内容
【题目】在某空间建立如图所示直角坐标系，并在该空间加上沿y轴负方向、磁感应强度大小为B的匀强磁场，和沿某个方向的匀强电场。一质量为m、带电量为+q（q＞0）的粒子从坐标原点O以初速度v沿x轴正方向射入该空间，粒子恰好能做匀速直线运动。不计粒子重力的影响，试求：
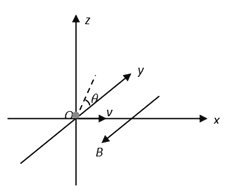
（1）所加电场强度E的大小和方向；
（2）若撤去电场，并改变磁感应强度的大小，使得粒子恰好能够经过坐标为（
，0，-a）的点，则改变后的磁感应强度B＇为多大？
若保持磁感应强度B不变，将电场强度大小调整为E＇，方向调整为平行于yOz平面且与y轴正方向成某个夹角θ，使得粒子能够在xOy平面内做匀变速曲线运动（类平抛运动）并经过坐标为（，a，0）的点，则E＇和tanθ各为多少？
【答案】（1）E=vB （2）
（3）
【解析】（1）由左手定则可知，带电粒子所受洛伦兹力沿z轴负方向，则有平衡条件可知，电场力沿z轴正方向，即电场强度沿z轴正方向，且有：
（3分）
解得：E=vB （1分）
（2）粒子运动的轨迹如图所示，由几何关系，有:
（2分）
解得粒子运动的半径为：r=2a （1分）
由牛顿第二定律，有：
（2分）
解得
（1分）
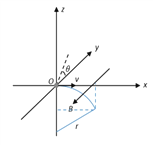
（3）由题意，电场力的一个分力沿z轴正方向平衡洛伦兹力，另一个分力沿y轴正方向提供类平抛运动加速度a0，如图所示。
则由平衡条件，有：
（3分）
由曲线运动规律，有：
（1分）
（1分）
其中：
（1分）
解得：
（1分）
（1分）
则有：
（1分）
（1分）
练习册系列答案
相关题目
