题目内容
12.孤立的两颗星球A、B构成双星系统,已知A、B质量之比mA:mB=1:3,那么它们的线速度之比vA:vB为( )| A. | 1:1 | B. | 3:1 | C. | 1:9 | D. | 9:1 |
分析 双星靠相互间的万有引力提供向心力,周期相等,据此求得双星的轨道半径之比,再根据线速度v=rω可知,双星的线速度之比即为轨道半径之比..
解答 解:双星绕连线上某点做匀速圆周运动,万有引力提供圆周运动向心力,两星的周期和角速度相同则有:
$G\frac{{m}_{A}{m}_{B}}{{(r}_{A}+{r}_{B})^{2}}={m}_{A}{r}_{A}{ω}^{2}={m}_{B}{r}_{B}{ω}^{2}$
可得$\frac{{r}_{A}}{{r}_{B}}=\frac{{m}_{B}}{{m}_{A}}$=$\frac{3}{1}$
据v=rω
可得:$\frac{{v}_{A}}{{v}_{B}}=\frac{{r}_{A}}{{r}_{B}}=\frac{3}{1}$
故选:B.
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,周期相等,角速度相等.根据m1r1=m2r2,得出轨道半径比,以及根据v=rω,得出线速度之比.

练习册系列答案
相关题目
3.在电磁学的发展过程中,许多科学家做出了贡献.下列说法正确的是( )
| A. | 欧姆提出了电场线和磁感线的概念 | |
| B. | 库伦发现了点电荷的作用规律,并通过油滴实验测定了元电荷的数值 | |
| C. | 奥斯特发现了电流磁效应,法拉第发现了电磁感应现象 | |
| D. | 安培发现了磁场对运动电荷的作用规律,洛伦兹发现了磁场对电流的作用规律 |
20.质量为m的物体,从静止开始以2g的加速度竖直知道向下运动h高度,那么( )
| A. | 物体的重力势能减少2mgh | B. | 物体的机械能保持不变 | ||
| C. | 物体的机械能增加2mgh | D. | 物体的动能增加2mgh |
7.下列说法正确的是( )
| A. | 伽利略认为自由落体运动可以认为是物体在倾角为90°的斜面上的运动,故根据铜球在斜面上的运动规律推出自由落体的运动规律,这里采用了实验和逻辑推理相结合的方法 | |
| B. | 两匹马比一匹马拉车跑得快,说明物体受力越大则速度就越大 | |
| C. | 人在沿直线加速前进的车厢内,竖直向上跳起后,将落在起跳点的后方 | |
| D. | 一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明:静止状态才是物体不受力时的“自然状态” | |
| E. | 神州号飞船返回舱返回地球,打开降落伞做减速直线运动的过程,返回舱处于超重状态 |
17.如图所示,真空中两等量异种电荷分别置于矩形PM边和QN边中点,则下列说法正确的是( )

| A. | P、N两点电势相同 | B. | P、N两点场强相同 | C. | P、Q两点电势相同 | D. | P、Q两点场强相同 |
1.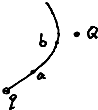 在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )
在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )
 在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )
在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )| A. | Ua>Ub,Eka>Ekb | B. | Ua>Ub,Eka<Ekb | C. | Ua<Ub,Eka>Ekb | D. | Ua<Ub,Eka<Ekb |
2. 如图所示,斜劈静止在水平地面上,有一物体沿斜劈表面向上运动,力F做的功与克服重力做的功相等,则下列判断中正确的是( )
如图所示,斜劈静止在水平地面上,有一物体沿斜劈表面向上运动,力F做的功与克服重力做的功相等,则下列判断中正确的是( )
 如图所示,斜劈静止在水平地面上,有一物体沿斜劈表面向上运动,力F做的功与克服重力做的功相等,则下列判断中正确的是( )
如图所示,斜劈静止在水平地面上,有一物体沿斜劈表面向上运动,力F做的功与克服重力做的功相等,则下列判断中正确的是( )| A. | 物体可能加速上滑 | |
| B. | 物体可能受三个力作用,且合力为零 | |
| C. | 斜劈如果受到地面的摩擦,则摩擦力的方向一定水平向左 | |
| D. | 撤去F后,斜劈可能不受地面的摩擦力 |
 如图,画有直角坐标系Oxy的白纸位于水平桌面上,M是放在白纸上的半圆形玻璃砖,其底面的圆心在坐标的原点,直边与x轴重合,OA是画在纸上的直线,P1、P2为竖直地插在直线OA上的两枚大头针,P3是竖直地插在纸上的第三枚大头针,α是直线OA与y轴正方向的夹角,β是直线OP3与轴负方向的夹角,只要直线OA画得合适,且P3的位置取得正确,测得角α和β,便可求得玻璃得折射率.某学生用上述方法测量玻璃的折射率.在他画出的直线OA上竖直插上了P1、P2两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃砖看到P1、P2的像,他应该采取的措施是在白纸上另画一条与y轴正方向的夹角较小的直线OA.若他已透过玻璃砖看到了P1、P2的像,在插大头针P3时,应使P3刚好能挡住P1、P2的像.若他已正确地测得了的α、β的值,则玻璃的折射率n=$\frac{sinβ}{sinα}$.(只需列出表达式,不需计算.)
如图,画有直角坐标系Oxy的白纸位于水平桌面上,M是放在白纸上的半圆形玻璃砖,其底面的圆心在坐标的原点,直边与x轴重合,OA是画在纸上的直线,P1、P2为竖直地插在直线OA上的两枚大头针,P3是竖直地插在纸上的第三枚大头针,α是直线OA与y轴正方向的夹角,β是直线OP3与轴负方向的夹角,只要直线OA画得合适,且P3的位置取得正确,测得角α和β,便可求得玻璃得折射率.某学生用上述方法测量玻璃的折射率.在他画出的直线OA上竖直插上了P1、P2两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃砖看到P1、P2的像,他应该采取的措施是在白纸上另画一条与y轴正方向的夹角较小的直线OA.若他已透过玻璃砖看到了P1、P2的像,在插大头针P3时,应使P3刚好能挡住P1、P2的像.若他已正确地测得了的α、β的值,则玻璃的折射率n=$\frac{sinβ}{sinα}$.(只需列出表达式,不需计算.)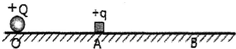 如图所示,绝缘水平地面上O点固定有电量为+Q的点电荷,一质量为m、电量为+q的可视为质点的小滑块与地面动摩擦因数为μ,从A点静止释放,最终停在B点,AB间距L,重力加速度为g,静电力常数为k,求:
如图所示,绝缘水平地面上O点固定有电量为+Q的点电荷,一质量为m、电量为+q的可视为质点的小滑块与地面动摩擦因数为μ,从A点静止释放,最终停在B点,AB间距L,重力加速度为g,静电力常数为k,求: