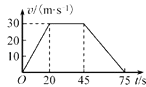
题目内容
【题目】如图所示，质量为3kg的木箱静止在光滑的水平面上，木箱内粗糙的底板正中央放着一个质量为1kg的小木块，小木块可视为质点．现使木箱和小木块同时获得大小为2m/s的方向相反的水平速度，小木块与木箱每次碰撞过程中机械能损失0.4J，小木块最终停在木箱正中央．已知小木块与木箱底板间的动摩擦因数为0.3，木箱内底板长为0.2m．求：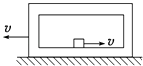
①木箱的最终速度的大小；
②小木块与木箱碰撞的次数．
【答案】解：①设最终速度为v，木箱与木块组成的系统动量守恒，以木箱的初速度方向为正方向，由动量守恒定律得：
Mv﹣mv=（M+m）v′，
代入数据得：v′=1m/s；
②对整个过程，由能量守恒定律可得：
mv2+ Mv2=△E+ （M+m）v′2，
设碰撞次数为n，木箱底板长度为L，
则有：n（μmgL+0.4）=△E，
代入数据得：n=6；
答：①木箱的最终速度的大小为1m/s；
②小木块与木箱碰撞的次数为6次．
【解析】①由动量守恒定律可以求出木箱的最终速度；②应用能量守恒定律与功的计算公式可以求出碰撞次数．
练习册系列答案
相关题目
