Question

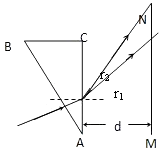
【题目】如图所示，有一截面是直角三角形的棱镜ABC，∠A=30°．它对红光的折射率为n1 ． 对紫光的折射率为n2 ． 在距AC边为d处有一与AC平行的光屏．现有由以上两种色光组成的很细的光束垂直AB边射入棱镜．

（1）红光和紫光在棱镜中的传播速度比为多少？
（2）为了使红光能从AC面射出棱镜，n1应满足什么条件？
（3）若两种光都能从AC面射出，求在光屏MN上两光点间的距离．

Answer 1

【答案】
（1）解：根据公式v= ，得

答：红光和紫光在棱镜中的传播速度比为n2：n1；

（2）解：由几何知识得到，红光射到AC面上的入射角i1=30°，要使红光能从AC面射出棱镜，必须使i1＜C，而sinC= ，得到sini1＜ ，解得n1＜2

答：为了使红光能从AC面射出棱镜，n1应满足的条件是n1＜2；

（3）解：设红光与紫光从AC面射出时的折射角分别为r1，r2．

根据折射定律得

n1= ，n2= ，又i1=i2=30°

又由几何知识得，在光屏MN上两光点间的距离△x=dtanr2﹣dtanr1

代入解得

）

答：若两种光都能从AC面射出，在光屏MN上两光点间的距离是 ．

【解析】（1）根据公式v= ，求出红光和紫光在棱镜中的传播速度之比．（2）由几何知识得到，红光射到AC面上的入射角i1=30°，要使红光能从AC面射出棱镜，必须使i1＜C，而sinC= 求n1应满足的条件．（3）根据折射定律分别求出两种光从AC面射出时的折射角，再由几何知识求解在光屏MN上两光点间的距离．
【考点精析】本题主要考查了光的折射的相关知识点，需要掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射才能正确解答此题．