题目内容
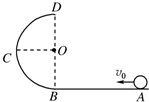 如图所示,AB为一段光滑绝缘水平轨道,BCD为一段光滑的圆弧轨道,半径为R,今有一质量为m、带电荷量为+q的绝缘小球,以速度v0从A点向B点运动,后又沿弧BC做圆周运动,到C点后由于v0较小,故难运动到最高点.如果当其运动至C点时,忽然在轨道区域加一匀强电场和匀强磁场,此时轨道弹力为零,且贴着轨道做匀速圆周运动,使其能运动到最高点,,求:
如图所示,AB为一段光滑绝缘水平轨道,BCD为一段光滑的圆弧轨道,半径为R,今有一质量为m、带电荷量为+q的绝缘小球,以速度v0从A点向B点运动,后又沿弧BC做圆周运动,到C点后由于v0较小,故难运动到最高点.如果当其运动至C点时,忽然在轨道区域加一匀强电场和匀强磁场,此时轨道弹力为零,且贴着轨道做匀速圆周运动,使其能运动到最高点,,求:(1)匀强电场的方向和强度;
(2)磁场的方向和磁感应强度.
(3)小球到达轨道的末端点D后,将做什么运动?
分析:当小球运动至C点时,在轨道区域加一匀强电场和匀强磁场,此时轨道弹力为零,且贴着轨道做匀速圆周运动,则重力与电场力平衡,则洛伦兹力提供向心力.根据力平衡分析电场强度大小和方向,由左手定则判断磁场方向.根据机械能守恒定律求出小球到C点时的速度,由牛顿定律求出B.小球到达轨道的末端点D后,受力情况没有变化,仍做匀速圆周运动.
解答:解:(1)由力平衡得mg=qE,得E=
,小球带正电,则电场强度方向竖直向上.
(2)A→C过程,由机械能守恒定律得
mgR+
=
m
vC=
又由qvCB=m
得 B=
=
由左手定则知,B的方向垂直于ABCD平面向外.
(3)小球由C到D的过程中轨道弹力为零,小球到达轨道的末端点D后,重力与电场力仍平衡,仍由洛伦兹力提供向心力,做匀速圆周运动.
答:(1)匀强电场的方向竖直向上,强度为
;
(2)磁场的方向垂直于ABCD平面向外,磁感应强度为
.
(3)小球到达轨道的末端点D后,将做匀速圆周运动.
| mg |
| q |
(2)A→C过程,由机械能守恒定律得
mgR+
| 1 |
| 2 |
| mv | 2 C |
| 1 |
| 2 |
| v | 2 0 |
|
又由qvCB=m
| ||
| R |
得 B=
| mvC |
| qR |
| m |
| qR |
|
由左手定则知,B的方向垂直于ABCD平面向外.
(3)小球由C到D的过程中轨道弹力为零,小球到达轨道的末端点D后,重力与电场力仍平衡,仍由洛伦兹力提供向心力,做匀速圆周运动.
答:(1)匀强电场的方向竖直向上,强度为
| mg |
| q |
(2)磁场的方向垂直于ABCD平面向外,磁感应强度为
| m |
| qR |
|
(3)小球到达轨道的末端点D后,将做匀速圆周运动.
点评:本题是重力场、电场和磁场的复合场问题,考查分析物体的运动过程,综合应用机械能守恒定律和牛顿定律的解题能力.

练习册系列答案
相关题目
 如图所示,AB为一段粗糙的1/4圆弧,半径为R,水平段BC长也为R.一个质量为m的物体与水平段BC间的动摩擦因数为μ,它从轨道的A点由静止滑下运动到C点恰好静止,则物体在圆弧上损失的机械能为( )
如图所示,AB为一段粗糙的1/4圆弧,半径为R,水平段BC长也为R.一个质量为m的物体与水平段BC间的动摩擦因数为μ,它从轨道的A点由静止滑下运动到C点恰好静止,则物体在圆弧上损失的机械能为( ) 如图所示,AB为一段粗糙的波浪形路面,且AB在同一水平面上,滑块以初速v沿粗糙曲面由A处滑到B处时速度大小为v1,以大小相同的初速沿粗糙曲面由B处滑到A处时速度大小为v2,则下面说法中正确的是( )
如图所示,AB为一段粗糙的波浪形路面,且AB在同一水平面上,滑块以初速v沿粗糙曲面由A处滑到B处时速度大小为v1,以大小相同的初速沿粗糙曲面由B处滑到A处时速度大小为v2,则下面说法中正确的是( )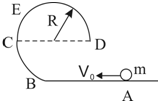 如图所示,AB为一段光滑绝缘水平轨道,BCD为一段光滑的圆弧轨道,半径为R,今有一质量为m、带电为+q的绝缘小球,以速度v0从A点向B点运动,后又沿弧BC做圆周运动,到C点后由于v0较小,故难运动到最高点.如果当其运动至C点时,忽然在轨道区域加一匀强电场和匀强磁场,使其能运动到最高点此时轨道弹力为0,且贴着轨道做匀速圆周运动,
如图所示,AB为一段光滑绝缘水平轨道,BCD为一段光滑的圆弧轨道,半径为R,今有一质量为m、带电为+q的绝缘小球,以速度v0从A点向B点运动,后又沿弧BC做圆周运动,到C点后由于v0较小,故难运动到最高点.如果当其运动至C点时,忽然在轨道区域加一匀强电场和匀强磁场,使其能运动到最高点此时轨道弹力为0,且贴着轨道做匀速圆周运动, (2013?盐城三模)如图所示,AB为一段弯曲轨道,固定在水平桌面上,与水平桌面相切于A点,B点距桌面的高度为h=0.6m,A、B两点间的水平距离为L=0.8m,轨道边缘B处有一轻小定滑轮,一根轻绳两端系着质量分别为m1与m2的物体P、Q,挂在定滑轮两边,P、Q可视为质点,且m1=2.0kg,m2=0.4kg.开始时P、Q 均静止,P紧靠B点,P释放后沿弯曲轨道向下运动,运动到A点时轻绳突然断开,断开后P沿水平桌面滑行距离x=1.25m停止.已知P与水平桌面间的动摩擦因数μ=0.25,g=10m/s2求:
(2013?盐城三模)如图所示,AB为一段弯曲轨道,固定在水平桌面上,与水平桌面相切于A点,B点距桌面的高度为h=0.6m,A、B两点间的水平距离为L=0.8m,轨道边缘B处有一轻小定滑轮,一根轻绳两端系着质量分别为m1与m2的物体P、Q,挂在定滑轮两边,P、Q可视为质点,且m1=2.0kg,m2=0.4kg.开始时P、Q 均静止,P紧靠B点,P释放后沿弯曲轨道向下运动,运动到A点时轻绳突然断开,断开后P沿水平桌面滑行距离x=1.25m停止.已知P与水平桌面间的动摩擦因数μ=0.25,g=10m/s2求: