Question

（2013?盐城三模）如图所示，AB为一段弯曲轨道，固定在水平桌面上，与水平桌面相切于A点，B点距桌面的高度为h=0.6m，A、B两点间的水平距离为L=0.8m，轨道边缘B处有一轻小定滑轮，一根轻绳两端系着质量分别为m₁与m₂的物体P、Q，挂在定滑轮两边，P、Q可视为质点，且m₁=2.0kg，m₂=0.4kg．开始时P、Q 均静止，P紧靠B点，P释放后沿弯曲轨道向下运动，运动到A点时轻绳突然断开，断开后P沿水平桌面滑行距离x=1.25m停止．已知P与水平桌面间的动摩擦因数μ=0.25，g=10m/s²求：
（1）P经过A点时的速度大小；
（2）P从B到A的过程中Q重力势能的增量；
（3）弯曲轨道对P的摩擦力做的功．

Answer 1

分析：（1）物体P在水平面上运动过程，运用动能定理求P经过A点时的速度．
（2）由几何知识求出Q上升的高度H，则Q重力势能的增量△E_P=mgH．
（3）由几何关系求出将P经过A点时AP段绳与水平方向的夹角，将此时P的速度进行分解得到Q点的速度，再对系统运用动能定理求摩擦力做功．

解答：解：（1）P在水平轨道上运动过程，根据动能定理得：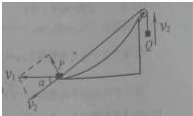
-μm₁gx=0-

1

2

m1

v

2 1

得：P经过A点时的速度v₁=

2μgs

=

2×0.25×10×1.25

m/s=2.5m/s
（2）P由B到A的过程中，Q上升的高度H=

h2+L2

=1m
则P从B到A的过程中Q重力势能的增量△E_P=mgH=4J
（3）设P经过A点时，Q的运动速度为v₂，将速度P的速度v₁进行分解如图．
则有v₂=v₁cosα
又sinα=

h

H

=0.6，得α=37°
对P、Q组成的系统，根据动能定理得：
   m₁gh-m₂gH+W_f=

1

2

m1

v

2 1

+

1

2

m2

v

2 2

代入数据解得，弯曲轨道对P的摩擦力做的功W_f=-0.95J．
答：
（1）P经过A点时的速度大小是2.5m/s；
（2）P从B到A的过程中Q重力势能的增量为4J；
（3）弯曲轨道对P的摩擦力做的功是-0.95J．

点评：本题是绳系的系统问题，根据动能定理和几何知识、速度分解进行分析求解，其中速度的分解，是绳端物体速度分解类型，要学会如何分解．