题目内容
【题目】小船在200m宽的河中横渡,水流速度为2m/s,船在静水中的航速是4m/s,求:
(1)当小船的船头始终正对对岸时,它将在何时、何处到达对岸?
(2)要使小船到达正对岸,应如何行驶(即船头与河岸的夹角为多大)?历时多长?
【答案】
(1)
解:小船参与了两个运动:随水漂流和船在静水中的运动.由分运动的等时性和独立性,
小船渡河时间等于垂直于河岸的分运动时间:
t=t1= ![]() =
= ![]() s=50 s,
s=50 s,
沿河流方向的位移x水=v水t=2×50 m=100 m,
即在正对岸下游100 m处靠岸.
(2)
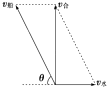
解:要小船垂直过河,即合速度应垂直于河岸,如图所示,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
所以θ=60°,即航向与岸上游成60°角;
渡河时间t= ![]() =
= ![]() =
= ![]() s=
s= ![]() s≈57.7 s
s≈57.7 s
【解析】(1)当船头始终正对对岸时,根据t= ![]() 求出渡河的时间,再由位移公式,求得到达对岸的位置;(2)要使小船到达正对岸,即合速度的方向与河岸垂直,根据平行四边形定则,求出合速度的大小,并由几何关系,结合矢量合成法则,即可求解.
求出渡河的时间,再由位移公式,求得到达对岸的位置;(2)要使小船到达正对岸,即合速度的方向与河岸垂直,根据平行四边形定则,求出合速度的大小,并由几何关系,结合矢量合成法则,即可求解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目