题目内容
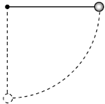如图所示，一小球用轻绳悬挂在某固定点，现将轻绳水平拉直，然后由静止开始释放小球．不计空气阻力，分析小球由静止开始运动到最低点的过程，以下结论正确的有（ ）| A、小球的速率不断增大 | B、重力的功率不断增大 | C、绳子的拉力不断增大 | D、绳子拉力的功率不断增大 |
分析：小球由静止开始运动到最低点的过程，只有重力做功，重力势能减小转化为动能．重力的功率等于重力与竖直分速度的税种，采用特殊位置法分析．绳子的拉力根据牛顿第二定律和向心力知识分析．功率的一般公式P=Fvcosα，α是v与F的夹角．
解答：解：A、小球由静止开始运动到最低点的过程中，重力做正功，重力势能转化为动能，所以小球的速率不断增大，故A正确．
B、小球刚释放时，速度为零，重力的功率为零；到达最低点时，重力与速度垂直，重力的功率也为零，而在运动过程中，重力与速度的夹角不垂直，重力有功率，所以重力的功率先增大后减小，故B错误．
C、设绳子与竖直方向的夹角为θ，小球运动过程中所需要的向心力由绳子拉力与重力沿绳子方向分力的合力提供，则有
T-mgcosθ=m
，得 T=mgcosθ+m
，因θ减小，cosθ增大，v增大，所以T增大，即绳子的拉力不断增大，故C正确．
D、绳子拉力与速度始终垂直，在速度方向上没有分力，所以拉力的功率始终为零，故D错误．
故选：AC
B、小球刚释放时，速度为零，重力的功率为零；到达最低点时，重力与速度垂直，重力的功率也为零，而在运动过程中，重力与速度的夹角不垂直，重力有功率，所以重力的功率先增大后减小，故B错误．
C、设绳子与竖直方向的夹角为θ，小球运动过程中所需要的向心力由绳子拉力与重力沿绳子方向分力的合力提供，则有
T-mgcosθ=m
| v2 |
| L |
| v2 |
| L |
D、绳子拉力与速度始终垂直，在速度方向上没有分力，所以拉力的功率始终为零，故D错误．
故选：AC
点评：解决本题关键要理解并掌握功率的一般公式P=Fvcosα，知道当α=90°时功率P=0，从而正确分析重力和拉力的功率．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
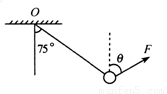
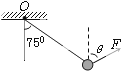（2011?湖南二模）如图所示，一小球用轻绳悬于?点，用力F拉住小球，使悬线保持偏离竖直方向75°角，且小球始终处于平衡状态，为了使F有最小值，F与竖直方向的夹角θ应该是（ ）
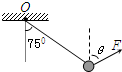如图所示，一小球用轻绳悬于O点，小华用力F拉住小球，使悬线保持偏离竖直方向75°角，且小球始终处于平衡状态．为了使F有最小值，则Fmin及此时Fmin与竖直方向的夹角θ分别是（ ）
