题目内容
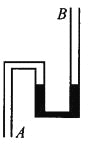
【题目】如图是形状为“2019”的竖直光滑轨道(轨道上端等高),其中数字“0”为半径R1=5m的圆,上半圆为单侧外轨道,轨道其余部分为管道。数字“9”上部分是一段四分之三的圆弧,圆的半径R2=1m:所有管道均平滑连接。现有一质量m=1kg的小球,小球的直径略小于管道直径,且小球直径远小于R1和R2大小。当小球以初速度v进入轨道,恰能通过“0”最高点A,并经过B、C点,最后从水平放置的CD管道的D点抛出,恰能无碰撞从管口E点进入倾角为θ的粗糙斜直管,然后小球沿斜直管下滑到底端。在斜直管中,假设小球受到阻力大小恒为其重量的0.3倍。已知E点距管底F的距离L=5m,求:

(1)小球通过“9”最高点B时对管道的弹力大小和方向;
(2)斜面的倾角的大小;
(3)小球在沿粗糙斜直管下滑到管底F时的速度大小。
【答案】(1)40N,方向向上;(2)53°;(3)![]() m/s
m/s
【解析】
(1)小球恰能通过“0”最高点A,由重力提供向心力,根据牛顿第二定律得:
![]()
故 ![]()
根据机械能守恒知,小球通过“9”最高点B时的速度为:
vB=vA=5![]() m/s
m/s
小球通过B点时,有:![]()
可得:N=40N,方向向下
根据牛顿第三定律知,小球对管道的弹力大小 N′=N=40N,方向向上。
(2)由A到D的过程,由机械能守恒得:![]()
解得 vD=3![]() m/s
m/s
由D点作平抛运动到E点的过程,有:
2R1﹣2R2=![]()
可得 vy=4![]() m/s
m/s
所以 tanθ=![]()
可得 θ=53°
(3)小球平抛运动到E点时的速度为:
![]()
由E点到F点的过程,由动能定理得:
(mgsin53°﹣kmg)L=![]()
解得:vF=10![]() m/s
m/s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目