��Ŀ����
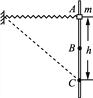
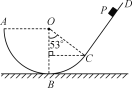
����Ŀ����ͼ��ʾ���뾶ΪR�Ĺ⻬Բ�����ABC��ֱ���ã�A��Բ��O�ȸߣ�BΪ�������͵㣬��Բ�������һ�ֲ�ֱ���CD�����ڵ�C��OC��OB�ļн�Ϊ53��.һ����Ϊm��С�����P���ɾ�ֹ��ʼ�»���PC�����Ϊ2R��������б��CD��Ķ�Ħ������Ϊ��.(��֪sin 53�㣽0.8��cos 53�㣽0.6���������ٶ�g)��
��1�������P�㻬��B������У��������ܵļ�������
��2�������P�㻬��C������У��˷�Ħ�������Ĺ���
��3��Ϊ��֤���鲻��A��������PC֮��������룮
���𰸡�(1) 2mgR.(2) ![]() ��mgR. (3)
��mgR. (3)![]() .
.
��������
�������֪���鹦���㡢���ܶ�����Ӧ�ã����ݹ��Ĺ�ʽ�����ܹ�ϵ����ɵá�
P�㵽����ĸ߶�����h����
![]()
��С���������ܵ����������Ĺ�
![]()
(2) ���P�㻬��C������У��˷�Ħ�������Ĺ�W������
![]()
(3) ��PC֮���������ΪL,��P�㵽A���ɶ��ܶ����ɵ�
![]()
���
![]()

��ϰ��ϵ�д�
 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�����Ŀ