题目内容
【题目】如图所示,一个半径为R的圆球,其重心不在球心O上,将它置于水平地面上,则平衡时球与地面的接触点为A;若将它置于倾角为30°的粗糙斜面上,则平衡时(静摩擦力足够大)球与斜面的接触点为B.已知AB的圆心角度数为60°,则圆球重心离球心O的距离是。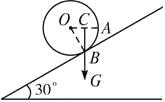
【答案】![]()
【解析】如图所示,当小球在斜面上处于静止时,小球的重力作用线一定通过B点,又知小球放在水平面上静止时,球与地面的接触点为A , 则其重力的作用线与OA重合,综上所述,球的重心应位于过B点的竖直线和OA线的交点C , 由几何关系知,∠CBO=30°,由此得,圆球重心距球心O的距离为: ![]() .
.
【考点精析】掌握重力是解答本题的根本,需要知道重力是由于地球对物体的吸引而产生的;重力的大小:地球表面G=mg;重力的方向:竖直向下(不一定指向地心);重心:物体的各部分所受重力合力的作用点,物体的重心不一定在物体上.

练习册系列答案
相关题目
【题目】“研究匀变速直线运动”的实验中,下列做法正确的是________.
A.先接通电源,再使纸带运动 |
B.先使纸带运动,再接通电源 |
C.将接好纸带的小车停在靠近滑轮处 |
D.将接好纸带的小车停在靠近打点计时器处 |