题目内容
【题目】如图所示，在光滑水平面上竖直固定一半径为R的光滑半圆槽轨道，其底端恰好与水平面相切，质量为m的小球以大小为V0的初速度经半圆槽轨道最低点B滚上半圆槽，小球恰能通过最高点C后落回到水平面上的A点．（不计空气阻力，重力加速度为g）求：
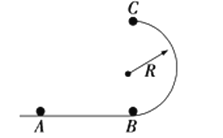
（1）小球通过B点时对半圆槽的压力大小；
（2）A、B两点间的距离．
【答案】（1）
（2）2R
【解析】试题分析：（1）对小球在B点时受力分析，根据牛顿第二定律求B受到的支持力，进而由牛顿第三定律得到B对圆槽的压力；（2）小球恰能通过最高点C，即重力提供向心力，根据牛顿第二定律求出小球在C点的速度，小球离开C点后作平抛运动，根据平抛运动的特点求出AB两点间的距离．
（1）在B点小球做圆周运动， 
，得
由牛顿第三定律知小球通过B点时对半圆槽的压力大是
；
（2）在C点小球恰能通过，故只有重力提供向心力，则
过C点小球做平抛运动： 
， 
， 
联立以上各式可得
．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
