��Ŀ����
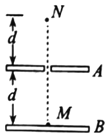
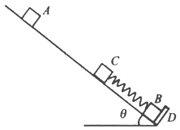
����Ŀ����ͼ�����Ϊ���Ĺ⻬б��˹̶�һ����ֱб��ĵ���Dб������A��B��C����������Ϊm����飨������Ϊ�ʵ㣩������B��Cͨ���ᵯ�������Ҿ����ھ�ֹ״̬��B�뵲��D�Ӵ�����A����C���Ϊd���ɾ�ֹ�ͷţ�A�˶���C��ʱ��C������ײ��ճ��һ�𡣵�A��C��������ߵ�ʱBǡ���뿪D�����ټ�����������֪A��C��ײ��ʱ�伫�̣��������ٶ�g����
(1)A��C��ײ���ٶȵĴ�С��
(2)���ɵľ���ϵ����
���𰸡�(1)![]() ��(2)
��(2)![]()
��������
(1)��A�˶���C��ʱ�ٶȵĴ�СΪv0�����ݻ�е���غ㶨����
![]()
��C��A��ײ���ٶȵĴ�Сv1����ײ���̸��ݶ����غ㶨����
![]()
�������
![]()
(2)�赯�ɵľ���ϵ��Ϊk�����ɳ�ʼ��ѹ����Ϊx1������
![]()
Bǡ���뿪D�����ټ�������ʱ�����ɵ��쳤��Ϊx2����ʱ��
![]()
���x1��x2����ĩ״̬����������ȡ���ABC���ϵͳ���ɻ�е���غ㶨����
![]()
���
![]()
��(1)A��C��ײ���ٶȵĴ�С![]() ��
��
(2)���ɵľ���ϵ��![]() ��
��

��ϰ��ϵ�д�
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
�����Ŀ