题目内容
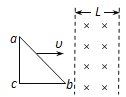
【题目】如图所示,一足够长的固定斜面,倾角θ=30°。质量为M=0.2kg的绝缘长板A.以初速度v0=3m/s,沿斜面匀速下滑。空间有一沿斜面向下的匀强电场,电场强度E=2.5×102N/C。质量为m=0Ikg,电量为q=+4×10-4C的光滑小物块B,轻放在A板表面上(整个过程未从上端滑出),此后经时间t=0.1s,撤去电场,当物块速度为v=8m/s时恰好离开板A,g取10m/s2。求:

(1)撤电场时物块B的动能EKB和ls内的电势能变化量△Ep
(2)撤电场时,板A的速度vA
(3)物块B在板A上运动的全过程,系统发热Q
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)先利用牛顿第二定律求出开始时B的加速度,再根据匀变速直线运动的规律求出B在电场方向的位移,最后通过功能关系得到B的电势能变化;
(2)先根据A匀速下滑得到动摩擦因素,再根据牛顿第二定律和根据匀变速直线运动的规律求出板A的速度;
(3)先利用动量守恒解得当A静止是B的速度,再根据根据匀变速直线运动的规律求出位移,最后求出系统的热量。
解:(1)开始时,B在板上加速: ![]()
撤去电场时,B的速度: ![]()
B的动能: ![]()
此时B在电场方向上的位移: ![]()
B的电势能变化量: ![]()
(2)A匀速下滑有, ![]()
B轻放上A,对A有: ![]()
撤去电场时,A的速度: ![]() ;
;
(3)如果B还在A上运动时:因为最大静摩擦力![]() ,当A速度减为0后,A将静止在斜面上
,当A速度减为0后,A将静止在斜面上
从撤去电场到A静止的过程中,A、B整体动量守恒: ![]()
当A速度为0时,可得B的速度: ![]()
因此,A静止后,B继续在A上加速运动直到离开
A的总位移: ![]()
系统发热: ![]() 。
。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目