Question

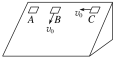
【题目】如图所示，一辆质量为M=6kg的平板小车A停靠在竖直光滑墙壁处，地面水平且光滑，一质量为m=2kg的小铁块B（可视为质点）放在平板小车A最右端，平板小车A上表面水平且与小铁块B之间的动摩擦因数μ=0.5，平板小车A的长度L=0.9m．现给小铁块B一个v0=5m/s的初速度使之向左运动，与竖直墙壁发生弹性碰撞后向右运动，求小铁块B在平板小车A上运动的整个过程中系统损失的机械能（g=10m/s2）．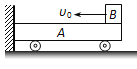

Answer 1

【答案】

【解析】设铁块向左运动到达竖直墙壁时的速度为v1，根据动能定理得： -μmgL=mv12-mv02，

代入数据解得：v1=4m/s
铁块与竖直墙发生弹性碰撞后向右运动，假设小铁块最终和平板车达到共速v2，规定向右为正方向，根据动量守恒定律得：mv1=（M+m）v2，

代入数据解得：v2=1m/s
设小铁块相对小车运动距离x与平板车达到共速，由能量守恒定律得：
-μmgx=（M+m）v22-mv12，

代入数据解得：x=1.2m
由于x＞L说明铁块在没有与平板车达到共速时就滑出平板车．
所以小铁块在平板上运动过程中系统损失的机械能为△E=2μmgL，解得：△E=18J．