Question

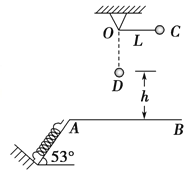
【题目】如图所示，在同一竖直平面内，一轻质弹簧一端固定，另一自由端恰好与水平线AB平齐，静止放于倾角为53°的光滑斜面上。一长为L＝9 cm的轻质细绳一端固定在O点，另一端系一质量为m＝1 kg的小球，将细绳拉至水平，使小球从位置C由静止释放，小球到达最低点D时，细绳刚好被拉断。之后小球在运动过程中恰好沿斜面方向将弹簧压缩，最大压缩量为x＝5 cm。（取g＝10 m/s2，sin 53°＝0．8，cos 53°＝0．6）求：

（1）细绳受到的拉力的最大值；

（2）D点到水平线AB的高度h；

（3）弹簧所获得的最大弹性势能Ep。

Answer 1

【答案】（1）30 N；（2）16 cm；（3）2．9 J

【解析】

试题分析：（1）小球由C到D，由机械能守恒定律得：

解得①

在D点，由牛顿第二定律得②

由①②解得F＝30 N

由牛顿第三定律知细绳所能承受的最大拉力为30 N。

（2）由D到A，小球做平抛运动vy2＝2gh③

④

联立解得h＝16 cm

（3）小球从C点到将弹簧压缩至最短的过程中，小球与弹簧系统的机械能守恒，即Ep＝mg（L＋h＋xsin 53°），代入数据解得：Ep＝2．9 J。