题目内容
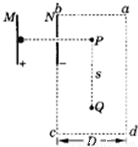
 如图所示,一个初速为零的带正电的粒子经过M、N两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd区域内出现大小不变、方向垂直于纸面且方向交替变化的匀强磁场.磁感强度B=0.4T.每经t=
如图所示,一个初速为零的带正电的粒子经过M、N两平行板间电场加速后,从N板上的孔射出,当带电粒子到达P点时,长方形abcd区域内出现大小不变、方向垂直于纸面且方向交替变化的匀强磁场.磁感强度B=0.4T.每经t=| π | 4 |
(1)加速电压为200V时带电粒子能否与中性粒子碰撞?
(2)画出它的轨迹.
(3)能使带电粒子与中性粒子碰撞,加速电压的最大值是多少?
分析:(1)洛伦兹力提供向心力,根据牛顿第二定律,推导出周期公式,并由动能定理求出速度,最后由半径公式来确定能否与中性粒子碰撞;
(2)根据左手定则,及几何关系,结合力与运动的关系,来确定运动轨迹;
(3)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压.
(2)根据左手定则,及几何关系,结合力与运动的关系,来确定运动轨迹;
(3)根据长度的关系,来确定相碰条件,从而求得最小半径,由半径公式与动能定理,共同求出加速电压.
解答: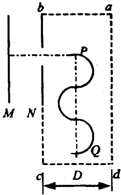 解:设带电粒子在磁场中做匀速圆周运动的半径为R,周期为T
解:设带电粒子在磁场中做匀速圆周运动的半径为R,周期为T
(1)根据洛伦兹力提供向心力,得周期公式,T=
代入数据,解得:T=
×10-3s
T恰好等于磁场变化周期的两倍,从P点起,磁场改变一次方向,
粒子恰好运动半个圆周.
由动能定理得:qU=
mv2
R=
故 R=
代入数据,
解得:R=0.5m
PQ=3m=6R,为半径的偶数倍,显然带电粒子能与中性粒子相碰
(2)轨迹如图
(3)相碰条件:PQ=2nR(n为正整数),且R≤
D,
即2nR=3m,R≤0.75m
n取最小值,则n=2
所以R′=0.75m
由R′=
,qUmmax=
mv′2,
代人数据,算得 U rnax=450V
答:(1)如果加速电压U=200V,带电粒子能与中性粒子碰撞;
(2)在答卷的图中画出U=200V时带电粒子的运动轨迹如右图.
(3)能使带电粒子与中性粒子碰撞,加速电压的最大值是450V.
 解:设带电粒子在磁场中做匀速圆周运动的半径为R,周期为T
解:设带电粒子在磁场中做匀速圆周运动的半径为R,周期为T(1)根据洛伦兹力提供向心力,得周期公式,T=
| 2πm |
| Bq |
| π |
| 2 |
T恰好等于磁场变化周期的两倍,从P点起,磁场改变一次方向,
粒子恰好运动半个圆周.
由动能定理得:qU=
| 1 |
| 2 |
R=
| mv |
| Bq |
|
代入数据,
解得:R=0.5m
PQ=3m=6R,为半径的偶数倍,显然带电粒子能与中性粒子相碰
(2)轨迹如图
(3)相碰条件:PQ=2nR(n为正整数),且R≤
| 1 |
| 2 |
即2nR=3m,R≤0.75m
n取最小值,则n=2
所以R′=0.75m
由R′=
| mv′ |
| Bq |
| 1 |
| 2 |
代人数据,算得 U rnax=450V
答:(1)如果加速电压U=200V,带电粒子能与中性粒子碰撞;
(2)在答卷的图中画出U=200V时带电粒子的运动轨迹如右图.
(3)能使带电粒子与中性粒子碰撞,加速电压的最大值是450V.
点评:考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,并掌握动能定理在此应用,同时还掌握几何关系的运用.

练习册系列答案
相关题目
 (2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B
(2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B 如图所示,一个质量为m,带电量是为-q的粒子(重力不计),从原点O处沿oy方向以初速v0射出,想加一个匀强磁场,使这个带电粒子能在xoy,平面内一开始就沿圆弧运动并通过a点[a点坐标为(x0,y0)],这个匀强磁场的方向如何?磁感应强度B多大?
如图所示,一个质量为m,带电量是为-q的粒子(重力不计),从原点O处沿oy方向以初速v0射出,想加一个匀强磁场,使这个带电粒子能在xoy,平面内一开始就沿圆弧运动并通过a点[a点坐标为(x0,y0)],这个匀强磁场的方向如何?磁感应强度B多大?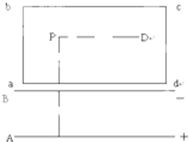 如图所示,一个初速为零的带正电荷的粒子经AB电场加速后,从B板上的小孔射出,进入长方形容器abcd,当粒子到达P点时,容器区域内立即出现大小不变,方向交替变化,但始终与纸面垂直的匀强磁场,磁感强度B=4T,粒子到达P点时,磁场方向指向纸外,且每经t=
如图所示,一个初速为零的带正电荷的粒子经AB电场加速后,从B板上的小孔射出,进入长方形容器abcd,当粒子到达P点时,容器区域内立即出现大小不变,方向交替变化,但始终与纸面垂直的匀强磁场,磁感强度B=4T,粒子到达P点时,磁场方向指向纸外,且每经t=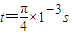 ,磁场方向变化一次.粒子到达P点时出现的磁场方向指向纸外,在Q处有一个静止的中性粒子,P、Q间距离s=3m.PQ直线垂直平分ab、cd.已知D=1.6M,带电粒子的荷质比为1.0×104C/kg,重力忽略不计.求
,磁场方向变化一次.粒子到达P点时出现的磁场方向指向纸外,在Q处有一个静止的中性粒子,P、Q间距离s=3m.PQ直线垂直平分ab、cd.已知D=1.6M,带电粒子的荷质比为1.0×104C/kg,重力忽略不计.求