题目内容
 (2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B
(2011?安庆二模)如图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B点相切,在圆轨道B点处开有一小孔,有一可看作质点的小球从斜面上距离地面高为h的A点无初速滚下,从B点进入圆轨道,所有摩擦不计.关于小球的运动情况,下述说法中正确的是( )
分析:小球不会脱离轨道有两种情况:1.在o点水平面以下来回滑动,2.能在竖直平面内做完整的圆周运动,这就要求小球能到达最高点,恰好到达最高点是个临界状态,根据机械能守恒定律及向心力公式即可求解.
解答:解:小球恰好过圆最高点时,只有重力提供向心力:
mg=m
小球由A运动到最高点的过程中机械能守恒,则
mg(h-2R)=
mv2
解得:
h=
所以当h≥
时,小球不会脱离轨道;
但是当h<R 时,小球在o点水平面以下来回滑动,小球也不会脱离轨道.
故选D.
mg=m
| v2 |
| R |
小球由A运动到最高点的过程中机械能守恒,则
mg(h-2R)=
| 1 |
| 2 |
解得:
h=
| 5R |
| 2 |
所以当h≥
| 5R |
| 2 |
但是当h<R 时,小球在o点水平面以下来回滑动,小球也不会脱离轨道.
故选D.
点评:该题主要考查了机械能守恒定律及圆周运动向心力公式的直接应用.解题时,应准确理解题意,注意考虑问题的全面性.

练习册系列答案
相关题目
 (2011?安庆二模)如图所示,在光滑的水平面上,一个质量为m的小球以速度v向东做匀速直线运动,小球运动的前方有一足够长的挡板,挡板与正东方向成300角.在某时刻加一水平恒力作用在小球上,小球经过路程L到达挡板时速度恰好为零,则所加恒力的大小是( )
(2011?安庆二模)如图所示,在光滑的水平面上,一个质量为m的小球以速度v向东做匀速直线运动,小球运动的前方有一足够长的挡板,挡板与正东方向成300角.在某时刻加一水平恒力作用在小球上,小球经过路程L到达挡板时速度恰好为零,则所加恒力的大小是( )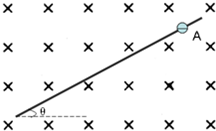 (2011?安庆二模)如图所示,空间存在垂直于纸面向里的磁感应强度为B的匀强磁场,场内有一绝缘的足够长的直杆,它与水平面的倾角为θ,一带电量为-q质量为m的带负电小球套在直杆上,从A点由静止沿杆下滑,小球与杆之间的动摩擦因数为μ,在小球以后的运动过程中,下列说法正确的是( )
(2011?安庆二模)如图所示,空间存在垂直于纸面向里的磁感应强度为B的匀强磁场,场内有一绝缘的足够长的直杆,它与水平面的倾角为θ,一带电量为-q质量为m的带负电小球套在直杆上,从A点由静止沿杆下滑,小球与杆之间的动摩擦因数为μ,在小球以后的运动过程中,下列说法正确的是( ) (2011?安庆二模)矩形导线框abcd放在磁场中,在外力控制下处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0~4s时间内,导线框ab边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是下列选项中的( )
(2011?安庆二模)矩形导线框abcd放在磁场中,在外力控制下处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0~4s时间内,导线框ab边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是下列选项中的( )