题目内容
 在光滑水平面上有质量均为lkg,半径均为5cm的A、B两个小球.如图所示,小球.A从很远处以水平速度v0=2m/s向右正对B球运动,从某时刻两小球间开始有F=2N的恒定引力作用.在经过一段时间后,两球间距缩小4m,从此时刻起,两球间开始有F'=2N的恒定斥力作用.
在光滑水平面上有质量均为lkg,半径均为5cm的A、B两个小球.如图所示,小球.A从很远处以水平速度v0=2m/s向右正对B球运动,从某时刻两小球间开始有F=2N的恒定引力作用.在经过一段时间后,两球间距缩小4m,从此时刻起,两球间开始有F'=2N的恒定斥力作用.(1)两球从开始有引力作用到开始有斥力作州经历时间为多少?
(2)为了使两球不相碰,开始有斥力时两球球心间距离应满足什么条件?
分析:(1)根据牛顿第二定律求得两球的加速度,由位移公式和位移之和等于4m列式求解时间.
(2)两球间开始有斥力后,A球先做匀减速运动,B球先做匀减速运动到速度为零,后再反方向加速,两球速度相等之前,两球间的距离一直减小,之后就逐渐增大,如果在两球速度相等之前不相碰,以后就不会相碰.根据速度公式和速度相等的关系列式,求解出两球开始时有斥力时的速度,运用运动学速度位移关系公式求解即可.
(2)两球间开始有斥力后,A球先做匀减速运动,B球先做匀减速运动到速度为零,后再反方向加速,两球速度相等之前,两球间的距离一直减小,之后就逐渐增大,如果在两球速度相等之前不相碰,以后就不会相碰.根据速度公式和速度相等的关系列式,求解出两球开始时有斥力时的速度,运用运动学速度位移关系公式求解即可.
解答:解:(1)当两球间有引力作用时,设两球的加速度大小分别为:aA和aB.由牛顿第二定律得:
aA=aB=
=
=2m/s2.
再由位移关系得:vAt+
aAt2+
aBt2=4
联立解得 t=1s
(2)设两球开始时有斥力作用时的速度大小分别为vA和vB,则
vA=v0+aAt,vB=aBt;
分析两球的运动情况:两球间开始有斥力后,A球先做匀减速运动,B球先做匀减速运动到速度为零,后再反方向加速,两球速度相等之前,两球间的距离一直减小,之后就逐渐增大,如果在两球速度相等之前不相碰,以后就不会相碰.设这段时间为t′,共同速度为v,开始有斥力时两球球心间距离为S,两球的加速度大小仍相同,并为aA=aB=2m/s2.
取vA的方向为正方向,v=vA-aAt′,v=-vB+aBt′
联立以上方程解得:vA=4m/s,vB=2m/s,v=1m/s
两球的位移分别为:SA=
,SB=
不相碰应满足:SA+SB+2r≤S
代入数据解得:S≥4.6m
答:
(1)两球从开始有引力作用到开始有斥力作州经历时间为是1s.
(2)为了使两球不相碰,开始有斥力时两球球心间距离应满足大于等于4.6m.
aA=aB=
| F |
| m |
| 2 |
| 1 |
再由位移关系得:vAt+
| 1 |
| 2 |
| 1 |
| 2 |
联立解得 t=1s
(2)设两球开始时有斥力作用时的速度大小分别为vA和vB,则
vA=v0+aAt,vB=aBt;
分析两球的运动情况:两球间开始有斥力后,A球先做匀减速运动,B球先做匀减速运动到速度为零,后再反方向加速,两球速度相等之前,两球间的距离一直减小,之后就逐渐增大,如果在两球速度相等之前不相碰,以后就不会相碰.设这段时间为t′,共同速度为v,开始有斥力时两球球心间距离为S,两球的加速度大小仍相同,并为aA=aB=2m/s2.
取vA的方向为正方向,v=vA-aAt′,v=-vB+aBt′
联立以上方程解得:vA=4m/s,vB=2m/s,v=1m/s
两球的位移分别为:SA=
| ||
| 2aA |
| ||
| 2aB |
不相碰应满足:SA+SB+2r≤S
代入数据解得:S≥4.6m
答:
(1)两球从开始有引力作用到开始有斥力作州经历时间为是1s.
(2)为了使两球不相碰,开始有斥力时两球球心间距离应满足大于等于4.6m.
点评:解决本题的关键是抓住两球的相互作用力是恒力,两球都做匀变速运动,根据牛顿第二定律和运动学公式分析两球的运动过程,抓住两球速度相同时,相距最远是关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
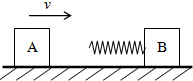 如图所示,在光滑水平面上有质量均为m的A和B两物体,B上装有一轻质弹簧,B原来静止,A以速度υ正对B滑行,当弹簧压缩到最大时,
如图所示,在光滑水平面上有质量均为m的A和B两物体,B上装有一轻质弹簧,B原来静止,A以速度υ正对B滑行,当弹簧压缩到最大时, 圆弧槽,圆弧槽底端的切线与A的上表面相平.现在A和C以共同速度v0冲向静止的B
圆弧槽,圆弧槽底端的切线与A的上表面相平.现在A和C以共同速度v0冲向静止的B