题目内容
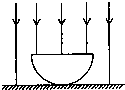 一个半径为R的玻璃半球,如图所示,平放在水平桌面上,已知玻璃的折射率为
一个半径为R的玻璃半球,如图所示,平放在水平桌面上,已知玻璃的折射率为| 2 |
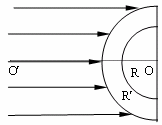
分析:光束垂直射入玻璃砖,方向不变进入玻璃砖,射到玻璃砖圆弧面时,发生折射,由全反射的知识画出光路图,用几何知识求暗环的半径即可求得其面积.
解答: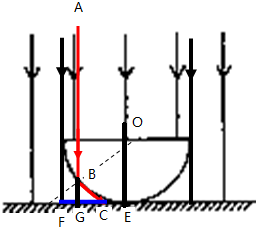 解:设临界角为C,则由sinC=
解:设临界角为C,则由sinC=
=
,得C=45°
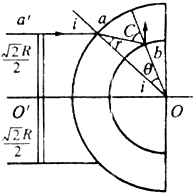
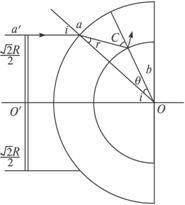
如图,取光线AB射到B点时恰好发生全反射,则入射角等于45°,折射角等于90°,AB光线右侧、OE左侧光线都能射到桌面上,则根据几何知识得:BG=R(1-
),FC=2BG=R(2-
)
则CE=R-FC=(
-1)R
故暗环的面积为S=πR2-πCE2=2(
-1)πR2
故选C
 解:设临界角为C,则由sinC=
解:设临界角为C,则由sinC=| 1 |
| n |
| 1 | ||
|
如图,取光线AB射到B点时恰好发生全反射,则入射角等于45°,折射角等于90°,AB光线右侧、OE左侧光线都能射到桌面上,则根据几何知识得:BG=R(1-
| ||
| 2 |
| 2 |
则CE=R-FC=(
| 2 |
故暗环的面积为S=πR2-πCE2=2(
| 2 |
故选C
点评:知道全反射临界角的含义及公式,能画出光路图是解决此类问题的关键.同时注意几何知识的应用.

练习册系列答案
相关题目
 (1)一列沿x轴正方向传播的简谐横波t时刻的波形图象如图1所示,已知该波的周期为T,a、b、c、d 为沿波传播方向上的四个质点.则下列说法中正确的是
(1)一列沿x轴正方向传播的简谐横波t时刻的波形图象如图1所示,已知该波的周期为T,a、b、c、d 为沿波传播方向上的四个质点.则下列说法中正确的是 如图所示.用折射宰
如图所示.用折射宰