题目内容
 (1)一列沿x轴正方向传播的简谐横波t时刻的波形图象如图1所示,已知该波的周期为T,a、b、c、d 为沿波传播方向上的四个质点.则下列说法中正确的是
(1)一列沿x轴正方向传播的简谐横波t时刻的波形图象如图1所示,已知该波的周期为T,a、b、c、d 为沿波传播方向上的四个质点.则下列说法中正确的是A.在t+
| T | 2 |
B.在t+2T时,质点d的加速度达到最大值
C.从t到t+2T的时间间隔内,质点d通过的路程为6cm
D.t时刻后,质点b比质点a先回到平衡位置
E.从t时刻起,在一个周期的时间内,a、b、c、d四个质点沿x轴通过的路程均为一个波长
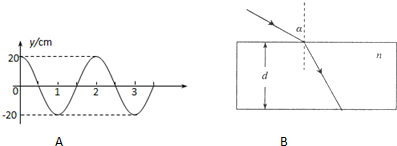
(2)投影仪的镜头是一个半球形的玻璃体(如图2),光源产生的单色平行光投射到平面上,经半球镜头折射后在光屏MN上形成一个圆形光斑.已知镜头半径为R,光屏MN到球心O的距离为d(d>3R),玻璃对该单色光的折射率为n,不考虑光的干涉和衍射.求光屏MN上被照亮的圆形光斑的半径.
分析:(1)在波传播的过程中,质点上下振动,一个周期内振动的路程等于4倍的振幅.
(2)设D点为发生全反射的临界点,结合sinC=
以及几何关系求出光屏MN上被照亮的圆形光斑的半径.
(2)设D点为发生全反射的临界点,结合sinC=
| 1 |
| n |
解答:解:(1)A、在t+
时,质点c运动到正向最大位移处,速度为零.故A错误.
B、经过1
T个周期,质点d开始振动,起振方向竖直向下,再经过
T到达正向最大位移处,所以在t+2T时,质点d的加速度达到最大值.故B正确.
C、经过1
T个周期,质点d开始振动,在剩余的
T内振动的路程等于3A=6cm.故C正确.
 D、根据“上下坡法”知a质点向上振动,b质点向上振动,b质点先回到平衡位置.故D正确.
D、根据“上下坡法”知a质点向上振动,b质点向上振动,b质点先回到平衡位置.故D正确.
E、质点上下振动,不随波迁移.故E错误.
故选B C D.
(2)在D点临界时
sinC=
cosC=R
=
=
=
而
=tgC
r=
=
?ctgC=(d-
)ctgC=(d-
)
=d
-nR
答:光屏MN上被照亮的圆形光斑的半径为d
-nR.
| T |
| 2 |
B、经过1
| 1 |
| 4 |
| 3 |
| 4 |
C、经过1
| 1 |
| 4 |
| 3 |
| 4 |
 D、根据“上下坡法”知a质点向上振动,b质点向上振动,b质点先回到平衡位置.故D正确.
D、根据“上下坡法”知a质点向上振动,b质点向上振动,b质点先回到平衡位置.故D正确.E、质点上下振动,不随波迁移.故E错误.
故选B C D.
(2)在D点临界时
sinC=
| 1 |
| n |
. |
| OF |
. |
| OF |
| R |
| cosC |
| R | ||||
|
| nR | ||
|
而
| ||
| r |
r=
| ||
| tgC |
. |
| O′F |
. |
| OF |
| nR | ||
|
| n2-1 |
=d
| n2-1 |
答:光屏MN上被照亮的圆形光斑的半径为d
| n2-1 |
点评:本题考查了振动和波动的关系、几何关系问题,对于几何光学问题,对数学的几何能力要求较高,要加强训练.

练习册系列答案
相关题目
 (2011?长春二模)[物理--选修3-4]
(2011?长春二模)[物理--选修3-4]
 ,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD=
,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD= ,求:
,求: