题目内容
如图所示.用折射宰n=
的玻璃做成一个外径为R的半球形空心球壳.一束与O′O平行的平行光射向此半球的外表面,若让一个半径为
R的圆形遮光板的圆心过O′O轴,并且垂直该轴放置则球壳内部恰好没有光线射入,问:
(1)临界光线射人球壳时的折射角r为多大?
(2)球壳的内径R′为多少?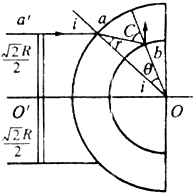
| 2 |
| ||
| 2 |
(1)临界光线射人球壳时的折射角r为多大?
(2)球壳的内径R′为多少?

(1)由题图和几何知识sini=

由折射率的定义式n=
联立解出r=30°
(2)对临界光线sinC=
在题图△oab中,由正弦定理:
=
联立解出R′=
R.
答:(1)临界光线射人球壳时的折射角r为30°.
(2)球壳的内径R′为
R.
| ||||
| R |

由折射率的定义式n=
| sini |
| sinr |
联立解出r=30°
(2)对临界光线sinC=
| 1 |
| n |
在题图△oab中,由正弦定理:
| R |
| sin(180°-C) |
| R′ |
| sinr |
联立解出R′=
| ||
| 2 |
答:(1)临界光线射人球壳时的折射角r为30°.
(2)球壳的内径R′为
| ||
| 2 |

练习册系列答案
相关题目
 如图所示.用折射宰
如图所示.用折射宰