题目内容
如图（甲）所示，在一块平板玻璃上放置一薄平凸透镜，在两者之间形成厚度不均匀的空气膜，让一束红光垂直入射到该装置上，结果在上方观察到如图（乙）所示的同心内疏外密的圆环状干涉条纹，称为牛顿环． 干涉现象是由于凸透镜下表面反射光和玻璃上表面反射光叠加形成的．如果换一个表面曲率半径更小的凸透镜，观察到的圆环半径将变小
变小
（填“变大”或“变小”），如果改用蓝光照射，观察到的圆环半径将变小
变小
（填“变大”或“变小”）．分析：从空气层的上下表面反射的两列光为相干光，当光程差为波长的整数倍时是亮条纹，当光程差为半个波长的奇数倍时是暗条纹．路程差等于空气膜厚度的两倍．使牛顿环的曲率半径越小，出现亮条纹的这一厚度向前移．从而得出圆环的半径的变化．
解答：解：当光程差为波长的整数倍时是亮条纹，当光程差为半个波长的奇数倍时是暗条纹．换一个表面曲率半径更小的凸透镜，出现亮条纹的这一厚度前移，知圆环的半径变小．用蓝光照射，波长变短，则出现亮条纹的这一厚度需前移，则圆环的半径变小．
故答案为：变小，变小．
故答案为：变小，变小．
点评：理解了牛顿环的产生机理就可顺利解决此类题目，故对物理现象要知其然更要知其所以然．
练习册系列答案
相关题目
如图（甲）所示，在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域，O点为该圆形区域的圆心，A点是圆形区域的最低点，B点是圆形区域最右侧的点．在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷，电荷的质量为m、电量为q，不计电荷重力、电荷之间的作用力．
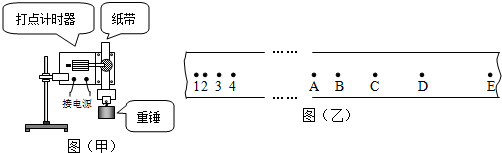纸带的第1个点和第2个点之间的距离都明显的大于2mm，于是他们选择了如图（乙）所示的一条点迹清晰且在