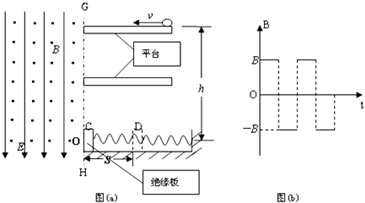
题目内容
一质量为m、带负电的电量为q的小物体，由静止沿倾角为θ的光滑绝缘斜面开始下滑，整个装置在一个足够大的匀强磁场中，磁场方向垂直于纸面向里，磁感应强度为B，如图所示．当物体滑到某一位置开始离开斜面，求：（1）物体离开斜面时的速度．
（2）物体在斜面上滑行的距离．
分析：（1）带电物体下滑到某一位置离开斜面，由此可知洛伦兹力垂直于斜面向上，根据左手定则判断带电物体的电性；对物体进行受力分析，当物体对斜面的压力为零时，物体开始离开斜面，由平衡条件求出物体此时的速度；
（2）由牛顿第二定律求出物体的加速度，然后由匀变速运动的速度位移公式求出物体在斜面上滑行的长度．
（2）由牛顿第二定律求出物体的加速度，然后由匀变速运动的速度位移公式求出物体在斜面上滑行的长度．
解答：解：（1）当小物体沿斜面加速下滑时，随着速度的增加，洛伦兹力逐渐增大，为了使小物体离开斜面，洛伦兹力的方向使必须垂直于斜面向上，可见，小物体带负电；
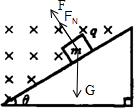
小物体沿斜面下滑时，受力如图所示：
由牛顿第二定律得：mgsinθ=ma，
故加速度：a=gsinθ，
洛伦兹力F=qvB，当FN=0，即qvB=mgcosθ，
v=
时，小物体开始离开斜面；
（2）由匀变速直线运动的速度位移公式可得：
v2-0=2aL，
则小物体在斜面上滑行的距离L=
．
答：（1）物体离开斜面时的速度为
．
（2）物体在斜面上滑行的长度是
．
小物体沿斜面下滑时，受力如图所示：
由牛顿第二定律得：mgsinθ=ma，
故加速度：a=gsinθ，
洛伦兹力F=qvB，当FN=0，即qvB=mgcosθ，
v=
| mgcosθ |
| qB |
（2）由匀变速直线运动的速度位移公式可得：
v2-0=2aL，
则小物体在斜面上滑行的距离L=
| m2gcos2θ |
| 2q2B2sinθ |
答：（1）物体离开斜面时的速度为
| mgcosθ |
| qB |
（2）物体在斜面上滑行的长度是
| m2gcos2θ |
| 2q2B2sinθ |
点评：解决本题的关键是正确地进行受力分析，抓住垂直于斜面方向上的合力为零时，物体开始离开斜面进行分析求解．
练习册系列答案
阅读快车系列答案
相关题目
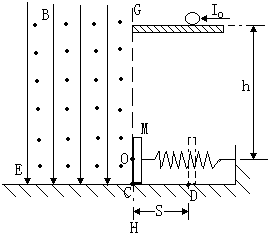如图所示，有一质量为m，带负电的小球静止在光滑绝缘的水平台上，平台距离质量为M 的绝缘板B的中心O高度为h，绝缘板放在水平地面上，板与地面间的动摩擦因数为μ，一轻弹簧一端连接在绝缘板的中心，另一端固定在墙面上．边界GH的左边存在着正交的匀强电场和匀强磁场，其电场强度为E，磁感应强度为B．现突然给小球一个水平向左的冲量，小球从平台左边缘垂直于边界GH进入复合场中，运动至O点处恰好与绝缘板发生碰撞，碰撞后小球恰能垂直反弹，而绝缘板向右从C点运动到D点，C、D间的距离为S，设小球与绝缘板碰撞过程无机械能损失．求：
