题目内容
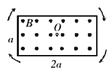
【题目】如图所示,ABCD为表示竖立放在场强为E=3×104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切A为水平轨道的一点,而且AB=R=0.2m,把一质量m=400g、带电q=10-4C的小球,放在水平轨道的A点上面由静止开始被释放后,在轨道的内侧运动.(g=10m/s2)
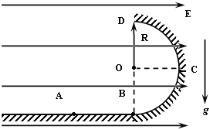
①它到达B点时的速度是多大?
②它到达C点时对轨道压力是多大?
③小球所能获得的最大动能是多少?
【答案】(1)![]() m/s(2)7N(3)0.8J
m/s(2)7N(3)0.8J
【解析】
(1)A至B过程中,由动能定理求解B点的速度;(2)根据动能定理求解小球到达C点的速度,根据牛顿第二定律求解到达C点时对轨道压力;(3)当小球到达平衡位置时速度最大,根据动能定理求解最大动能.
①设小球在B点速度为VB,则A至B过程中,由动能定理有
![]()
解得vB=![]() m/s
m/s
②设小球在C点的速度大小是vc,则对于小球由A→C的过程中,应用动能定律![]()
计算得出vc=![]()
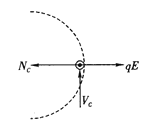
小球在C点时受力分析如图,应满足![]()
计算得出![]()
由牛顿第三定律可以知道小球对轨道的压力为7N.
③由mg=4N,Eq=3N.
设小球与O点连线与竖直方向OB的夹角为θ时动能为![]()
则![]()
![]()
解得![]() =0.8J
=0.8J

【题目】利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差.
(1)应该选择的实验电路是图1中的_____(选项“甲”或“乙”).

(2)现有电流表(0﹣0.6A)、开关和导线若干,以及以下器材:
A.电压表(0﹣15V) B.电压表(0﹣3V)
C.滑动变阻器(0﹣50Ω) D.滑动变阻器(0﹣500Ω)
实验中电压表应选用_____;滑动变阻器应选用_____;(选填相应器材前的字母)
(3)某位同学记录的6组数据如下表所示,其中5组数据的对应点已经标在图2的坐标纸上,请标出余下一组数据的对应点,并画出U﹣I图线._____
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U(V) | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I(A) | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
(4)根据(3)中所画图线可得出干电池的电动势E=_____v,内电阻r=_____Ω
(5)实验中,随着滑动变阻器滑片的移动,电压表的示数U以及干电池的输出功率P都会发生变化.各示意图中正确反映P﹣U关系的是_____.
A、 B、
B、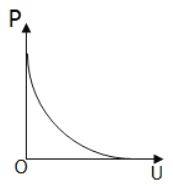
C、 D、
D、