Question

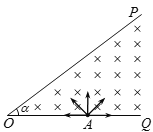
【题目】如图所示，从O点引出的两条射线OP、OQ，在两射线夹角α＝37的区域内存在着垂直于纸面向里的匀强磁场，磁感应强度B＝0.25T，边界上有磁场，且磁场区域足够大．A为射线OQ上离O点距离s＝10cm处的一点，大量相同的带负电粒子以相同的速率经过A点，在纸面内沿不同方向射入磁场，粒子质量m＝3×10－7 kg、电荷量q＝－1×10－2C、速率v＝5×102m/s，不计粒子重力、粒子间的相互作用，sin37＝0.6．求：

(1)粒子在磁场中运动的轨道半径r；

(2)能从射线OP射出磁场的粒子中，在磁场中运动的最短时间t（结果用含π的代数式表达）．

Answer 1

【答案】（1）6cm（2）

【解析】

（1）粒子在磁场中做匀速圆周运动，有

代入数据得：r＝6cm

（2）因粒子在磁场中运动的轨道半径是固定的，只有粒子在磁场中做圆周运动的弧长（或对应的弦长）最短时，其运动时间最短．过A作垂直于OP的线段AD，当粒子沿圆弧从D点射出磁场时，弦长最短，设其对应的圆心为O，其轨迹如图所示

所以，ADO为等边三角形

圆心角：

运动周期：

最短时间：