题目内容
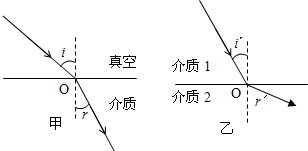
如图甲所示,真空中一束波长为λ的单色光射向某一透明介质,若入射角i=45°,折射角r=30°,则该单色光在介质中的波长λ?= ;一声波由介质1进入介质2,其波线如图乙所示,入射角i?=30°,若该声波在介质1中波速为340m/s,在介质2中的波速为340
m/s,则折射角r?为 .
| 3 |

分析:根据光的折射定律求出折射率的大小,抓住光的频率不变,通过波速求出波长的关系.根据折射定律求出折射角r′的大小.
解答:解:根据折射定律得,n=
=
.
则光在介质中的速度v=
,因为光从真空进入介质,频率不变,有
=
,解得λ′=
λ=
=
.
根据
=
=
解得r′=60°.
故答案为:
,60°
| sin45° |
| sin30° |
| 2 |
则光在介质中的速度v=
| c |
| n |
| c |
| λ |
| v |
| λ′ |
| v |
| c |
| λ |
| n |
| ||
| 2 |
根据
| sini′ |
| sinr′ |
| v1 |
| v2 |
| 1 | ||
|
解得r′=60°.
故答案为:
| ||
| 2 |
点评:解决本题的关键掌握折射定律,以及知道光从一种介质进入另一种介质,频率不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

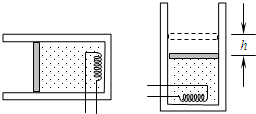 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.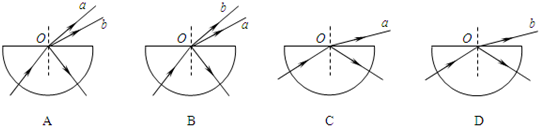
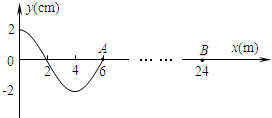
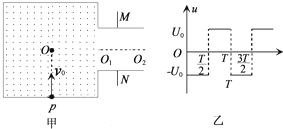 如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)
如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计) 
