题目内容
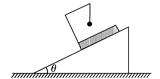
【题目】如图是某“吃货”设想的“糖炒栗子”神奇装置:炒锅的纵截面与半径R=1.6 m的光滑半圆弧轨道位于同一竖直面内,炒锅纵截面可看作是长度均为L =2.5 m的斜面AB、CD和一小段光滑圆弧BC平滑对接组成。假设一栗子从水平地面上以水平初速v0射人半圆弧轨道,并恰好能从轨道最高点P飞出,且速度恰好沿AB方向从A点进入炒锅。已知两斜面的倾角均为θ=37°,栗子与两斜面之间的动摩擦因数均为![]() ,粟子在锅内的运动始终在图示纵截面内,整个过程粟子质量不变,重力加速度取g=10 m/s2,sin37°=0.6,cos37°=0.8。求:
,粟子在锅内的运动始终在图示纵截面内,整个过程粟子质量不变,重力加速度取g=10 m/s2,sin37°=0.6,cos37°=0.8。求:
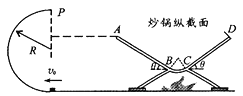
(1)栗子的初速度v0及A点离地高度h;
(2)栗子在斜面CD上能够到达的距C点最大距离x。
【答案】(1)2.75m;(2)2.22m
【解析】(1)设栗子质量为m,在P点的速度为vP,在A点的速度为vA.A点离地高度为h
栗子沿圆弧轨道运动至P点的过程中
由机械能守恒定律有![]()
恰能过P点,满足的条件为:![]()
代入数据解得: ![]() ,
,![]() ;
;
栗子从P至A做平抛运动,在A点的速度方向沿AB
竖直分速度:![]()
由平抛运动规律,栗子从P至A下落的高度为:![]()
又:![]()
代人数据解得:![]()
(2)栗子第一次在斜面CD上运动的过程中可达到距C点的最大距离
栗子在A点的速度为:![]()
由动能定理有: ![]()
代入数据解得: ![]() .
.

练习册系列答案
相关题目