��Ŀ����
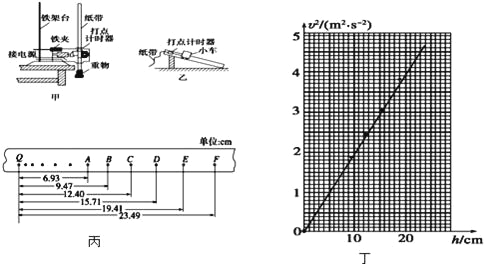
����Ŀ����ͼ�������㹻���ҹ⻬��ƽ�н����������L��0.1m���ã���б��![]() ,
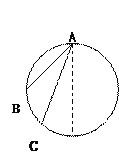
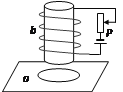
,![]() .�¶˽��е���R=0.2������S���ڵ����ϰ벿���б߽��뵼�촹ֱ����ǿ�ų������дų�������Ϊd=2m���ų��������Ŵų��������ų��������ֱ�ڵ���ƽ�棬�ų����ĴŸ�Ӧǿ�Ⱥ�ΪB2=1T���ų����ĴŸ�Ӧǿ��B1��0��1s����ʱ��������ӣ�1s֮��Ϊijһ�㶨ֵ��t=0ʱ���պ�s��ͬʱ�ڴų����з���������ͬ��������Ϊ0.1kg�ĵ������λ����ͼ������ҲΪR����������������պô��ھ�ֹ״̬��t=1sʱ���Ͽ�S�����ֵ�a���ս���ų���ʱ������ʼ�����˶���b����Ҫ���ų���ʱ��б�����µļ��ٶ�Ϊ
.�¶˽��е���R=0.2������S���ڵ����ϰ벿���б߽��뵼�촹ֱ����ǿ�ų������дų�������Ϊd=2m���ų��������Ŵų��������ų��������ֱ�ڵ���ƽ�棬�ų����ĴŸ�Ӧǿ�Ⱥ�ΪB2=1T���ų����ĴŸ�Ӧǿ��B1��0��1s����ʱ��������ӣ�1s֮��Ϊijһ�㶨ֵ��t=0ʱ���պ�s��ͬʱ�ڴų����з���������ͬ��������Ϊ0.1kg�ĵ������λ����ͼ������ҲΪR����������������պô��ھ�ֹ״̬��t=1sʱ���Ͽ�S�����ֵ�a���ս���ų���ʱ������ʼ�����˶���b����Ҫ���ų���ʱ��б�����µļ��ٶ�Ϊ![]() ����
����
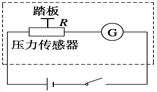
(1)1sǰ�ų����ĴŸ�Ӧǿ��B1�ı仯�ʣ�
(2) 1s֮�ų����ĴŸ�Ӧǿ��B1��
(3) b�������������еķ�������

���𰸡�(1)1.0A(2)1T��3��![]()
��������(1)��![]() ʱ��ͨ�������ĵ�����ͬ�������������ֹ��
ʱ��ͨ�������ĵ�����ͬ�������������ֹ�� ![]() ��
�� ![]() ��
��  ��
�� ![]() �������ϸ�ʽ���
�������ϸ�ʽ���![]() ��
�� ![]() ��
��
(2)t0ʱ�̣��Ͽ�s������һ���ڴų������ȼ����»�d��a������ų������������и�Ÿ��ߣ�������Դ������������ȣ�������ͬ�������������ʼ�������˶�������b��ʼ���ڴų����У����θ�Ӧ������Сһ��������t0֮�ų����ĴŸ�Ӧǿ��B1��B2��1T��
(3) a������ų���ʱ�����˶����ٶ�Ϊv0������һ���ڴų������ȼ����»�d�Ĺ��̻�е���غ㣺 ![]() �����
�����![]() ����a�����ų�Iʱ��b���պý���ų�I��Ҫ��ʼ��������˶���ֱ�����ų���ʱ�ļ��ٶ���
����a�����ų�Iʱ��b���պý���ų�I��Ҫ��ʼ��������˶���ֱ�����ų���ʱ�ļ��ٶ���![]() ������ţ�ٵڶ����ɿ�֪
������ţ�ٵڶ����ɿ�֪![]() ��
�� ![]() �����
�����![]() ��
��
b����t0ǰ�� ![]()
a��b���ֱ��ڴų������������٣�b��������![]()
b���ڴų����б���٣�b��������
![]()
b�������������еķ�����![]()