题目内容
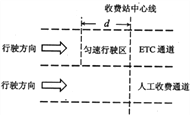
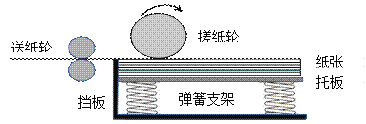
【题目】如图所示，是某打印机的分纸、送纸机构的简化装置图。一叠纸由带有弹簧支架的托板托起，压在搓纸轮下方，纸张前端与挡板右侧面平齐。每一次输纸指令发出后，搓纸轮的转速可在时间t1内从零均匀增加到n（单位：转/秒），之后匀速转动至本次输纸结束，搓纸轮的直径为D。正常情况下搓纸轮与最上面的纸张间不会发生相对滑动，要求输纸指令发出后，搓纸轮必须在时间t2内（t2>t1）将最上面的一张纸的前端送达两送纸轮的切点处。
（1）求两送纸轮的切点与纸张前端的距离x。
（2）如果已知每张纸的质量均为m，纸张与纸张间的动摩擦因数均为
，重力加速度为g，搓纸轮对纸张的压力恒为N。为了确保每次成功输送一张纸，搓纸轮与纸张间的动摩擦因数
应该满足什么条件？ （假设最大静摩擦力等于滑动摩擦力，忽略一张纸的重力）
【答案】(1)
；(2)
【解析】(1) 搓纸轮匀速转动时边缘的线速度为
根据题意，搓纸轮带动纸张先做匀加速运动，后匀速运动。
匀加速运动的位移为
匀速运动的位移为 
故两送纸轮的切点与纸张前端的距离为
；
(2) 第一、二张纸之间的摩擦力为滑动摩擦力f1，满足
设搓纸轮对最上面的第一张纸的静摩擦力为f2， 则
对最上面的那一张纸，要求在时间t1内加速到v，根据牛顿第二定律
且 
联立得
练习册系列答案
相关题目
