题目内容
18.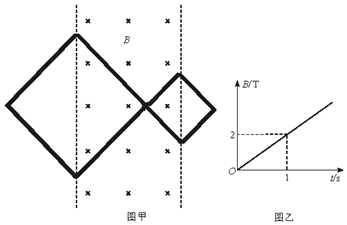 一根阻值12Ω的金属导线绕成如图甲形状的闭合回路,大正方形边长0.4m,小正方形边长0.2m,共10匝.放在粗糙的水平桌面上,两正方形对角线间存在竖直向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示,整个过程中线框始终未动.求闭合回路
一根阻值12Ω的金属导线绕成如图甲形状的闭合回路,大正方形边长0.4m,小正方形边长0.2m,共10匝.放在粗糙的水平桌面上,两正方形对角线间存在竖直向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示,整个过程中线框始终未动.求闭合回路(1)产生的感应电动势;
(2)电功率;
(3)第1s末受到的摩擦力.
分析 (1)根据法拉第电磁感应定律求解感应电动势,其中两个回路电动势方向相反,所以相互抵消;
(2)根据$P=\frac{{E}_{\;}^{2}}{R}$求出线框的电功率;
(3)求出线框的电流,求出在磁场中的两条边所受的安培力的合力,摩擦力方向与安培力的方向相反,大小相等;
解答 解:(1)据法拉第电磁感应定律有为:
$E=N\frac{△φ}{△t}=N\frac{△BS}{△t}$
得:$E=N\frac{△B}{△t}S$═$10×\frac{2}{1}×\frac{1}{2}×(0.{4}_{\;}^{2}-0.{2}_{\;}^{2})$=1.2V
(2)电功率为:$P=\frac{{E}_{\;}^{2}}{R}=\frac{1.{2}_{\;}^{2}}{12}=0.12W$
(3)线框中的电流为:$I=\frac{E}{R}=\frac{1.2}{12}A=0.1A$
在磁场中的两条边受到的力垂直于线框,大小相等,互成90°,每条边受到的力为:
F=NBIL=10×2×0.1×(0.4+0.2)N=1.2N
安培力的合力为:$F′=\sqrt{2}F=\sqrt{2}×1.2=1.7N$
摩擦力为:f=F=1.70N
答:(1)产生的感应电动势为1.2V;
(2)电功率为0.12W;
(3)第1s末受到的摩擦力为1.70N
点评 本题考查法拉第电磁感应、电功率、安培力公式等知识点,关键是要注意图中有效面积不是两个在磁场中的三角形面积之和,而是面积之差,因为感应电动势方向相反.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.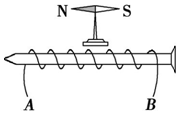 小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )
小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )
 小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )
小李同学用铁钉与漆包线绕成电磁铁,当接通电路后,放在其上方的小磁针 N 极立即转向左侧,如图所示.则此时( )| A. | 导线 A 端接电池负极 | |
| B. | 铁钉内磁场方向向右 | |
| C. | 铁钉左端为电磁铁的 N 极 | |
| D. | 小磁针所在位置的磁场方向水平向右 |
9.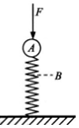 如图所示,下端固定的竖直轻弹簧上连接着质量为m的小球A,在竖直向下力F作用下,弹簧被压缩到B点(弹簧弹性限度内),小球静止,此时力F=2mg.现突然撤去力F,小球将向上弹起直至速度为零,不计空气阻力,重力加速度为g;则小球在上升的过程中( )
如图所示,下端固定的竖直轻弹簧上连接着质量为m的小球A,在竖直向下力F作用下,弹簧被压缩到B点(弹簧弹性限度内),小球静止,此时力F=2mg.现突然撤去力F,小球将向上弹起直至速度为零,不计空气阻力,重力加速度为g;则小球在上升的过程中( )
 如图所示,下端固定的竖直轻弹簧上连接着质量为m的小球A,在竖直向下力F作用下,弹簧被压缩到B点(弹簧弹性限度内),小球静止,此时力F=2mg.现突然撤去力F,小球将向上弹起直至速度为零,不计空气阻力,重力加速度为g;则小球在上升的过程中( )
如图所示,下端固定的竖直轻弹簧上连接着质量为m的小球A,在竖直向下力F作用下,弹簧被压缩到B点(弹簧弹性限度内),小球静止,此时力F=2mg.现突然撤去力F,小球将向上弹起直至速度为零,不计空气阻力,重力加速度为g;则小球在上升的过程中( )| A. | 小球先向上做匀加速运动再做匀减速运动 | |
| B. | 当弹簧恢复到原长时,小球速度最大 | |
| C. | 撤去力F瞬间,小球加速度大小为2g | |
| D. | 小球的加速度先减小后增大 |
6.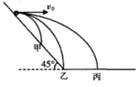 如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )
如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )
 如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )
如图所示,甲、乙、丙三个小球从倾角为45°的斜面上同一点开始平抛运动,甲球落到斜面上,乙球落到斜面底端,丙球落到水平地面上,如果甲、乙、丙三个小球在水平方向上的位移之比为1:2:3,则甲、乙、丙三个小球做平抛运动的初速度之比为( )| A. | $\sqrt{2}$:2:3 | B. | 1:2:3 | C. | $\frac{1}{2}$:2:3 | D. | $\frac{1}{\sqrt{2}}$:2:3 |
13.下列有关原子物理学的说法正确的是( )
| A. | 研制核武器的钚239(${\;}_{94}^{239}$Pu)由铀239(${\;}_{92}^{239}$U)经过2次β衰变而产生 | |
| B. | 天然放射现象中产生的射线都能在电场或磁场中发生偏转 | |
| C. | 若发生了光电效应且入射光的频率一定时,光强越强,单位时间内逸出的光电子数就越多 | |
| D. | 若氢原子核外电子从激发态n=3跃迁到基态发出的光子刚好能使某金属发生光电效应,则从激发态n=2跃迁到基态发出的光子一定能使该金属发生光电效应 |
3.火星探测器沿火星近地圆轨道飞行,其周期和相应的轨道半径分别为T0和R0,火星的一颗卫星在其圆轨道上的周期和相应的轨道半径分别为T和R,则下列关系正确的是( )
| A. | lg($\frac{T}{{T}_{0}}$)=$\frac{3}{2}$lg($\frac{R}{{R}_{0}}$) | B. | lg($\frac{T}{{T}_{0}}$)=2lg($\frac{R}{{R}_{0}}$) | C. | lg($\frac{T}{{T}_{0}}$)=$\frac{3}{2}$lg($\frac{{R}_{0}}{R}$) | D. | lg($\frac{T}{{T}_{0}}$)=2lg($\frac{{R}_{0}}{R}$) |
10.火星表面很接近地球,是将来人类可能的居住地.已知火星的质量约为地球质量的$\frac{1}{9}$,火星的半径约为地球半径的$\frac{1}{2}$,火星的自转周期约为24h,已知地球表面重力加速度为9.8m/s2,由此可估算出( )
| A. | 火星表面的重力加速度约为9.8m/s2 | |
| B. | 环绕火星运动的卫星的最大速度约为3.7km/s | |
| C. | 火星的平均密度约为地球平均密度的一半 | |
| D. | 火星同步卫星的运动半径约等于地球同步卫星运动的半径 |
7.火星的半径约为3.4×103km,表面重力加速度约为3.7m/s2.若发射一颗火星探测卫星,卫星轨道为距离火星表面600km的圆周,该卫星环绕火星飞行的线速度约为( )
| A. | 1.0×102m/s | B. | 1.5×102m/s | C. | 3.3×103m/s | D. | 3.8×103m/s |
8. “轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,以延长卫星的使用寿命,如图所示,“轨道康复者”与一颗地球同步卫星在同一平面内,绕地球以相同的方向做匀速圆周运动,“轨道康复者”与同步卫星的轨道半径之比为1:4,若不考虑“轨道康复者”与同步卫星之间的万有引力,则下列说法正确的是( )
“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,以延长卫星的使用寿命,如图所示,“轨道康复者”与一颗地球同步卫星在同一平面内,绕地球以相同的方向做匀速圆周运动,“轨道康复者”与同步卫星的轨道半径之比为1:4,若不考虑“轨道康复者”与同步卫星之间的万有引力,则下列说法正确的是( )
 “轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,以延长卫星的使用寿命,如图所示,“轨道康复者”与一颗地球同步卫星在同一平面内,绕地球以相同的方向做匀速圆周运动,“轨道康复者”与同步卫星的轨道半径之比为1:4,若不考虑“轨道康复者”与同步卫星之间的万有引力,则下列说法正确的是( )
“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,以延长卫星的使用寿命,如图所示,“轨道康复者”与一颗地球同步卫星在同一平面内,绕地球以相同的方向做匀速圆周运动,“轨道康复者”与同步卫星的轨道半径之比为1:4,若不考虑“轨道康复者”与同步卫星之间的万有引力,则下列说法正确的是( )| A. | “轨道康复者”在图示轨道上运行周期为6h | |
| B. | “轨道康复者”线速度大小是同步卫星的2倍 | |
| C. | 站在赤道上的人观察到“轨道康复者”向西运动 | |
| D. | 为实施对同步卫星的拯救,“轨道康复者”需从图示轨道加速 |