题目内容
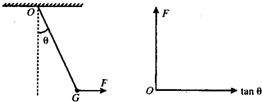 如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球,球处于静止状态,现对球施加一个方向始终保持水平的外力F,使球缓慢地移动,在移动过程中的每一时刻,均可认为球处于平衡状态.若要保证轻绳不被拉断,绳与竖直方向夹角θ 必须满足θ≤60°,求:
如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球,球处于静止状态,现对球施加一个方向始终保持水平的外力F,使球缓慢地移动,在移动过程中的每一时刻,均可认为球处于平衡状态.若要保证轻绳不被拉断,绳与竖直方向夹角θ 必须满足θ≤60°,求:?(1)轻绳可以承受的拉力FT的最大值;
?(2)在F-tanθ 坐标系中画出外力F与tanθ的关系图象.
分析:(1)分析小球的受力情况,由平衡条件得出轻绳的拉力与θ的关系,由数学知识求解拉力FT的最大值;
(2)由平衡条件得出F与tanθ 的关系式,确定出F大小的范围,画出F与tanθ的关系图象.
(2)由平衡条件得出F与tanθ 的关系式,确定出F大小的范围,画出F与tanθ的关系图象.
解答: 解:(1)钢球的受力情况如图所示.
解:(1)钢球的受力情况如图所示.
?由平衡条件F合=0,则有
?FT=
?当θ=60°时,轻绳刚好不被拉断,即轻绳可以承受的拉力FT的最大值为2G.
?(2)由平衡条件则得,F=Gtanθ
?当θ=0时,F=0
?当θ=60°时,F=
G
?所以,F的取值范围为0≤F≤
G,F与tanθ的关系图象如图.
答:(1)轻绳可以承受的拉力FT的最大值;
?(2)外力F与tanθ的关系图象如图所示.
 解:(1)钢球的受力情况如图所示.
解:(1)钢球的受力情况如图所示.?由平衡条件F合=0,则有
?FT=
| G |
| cosθ |
?当θ=60°时,轻绳刚好不被拉断,即轻绳可以承受的拉力FT的最大值为2G.
?(2)由平衡条件则得,F=Gtanθ
?当θ=0时,F=0
?当θ=60°时,F=
| 3 |
?所以,F的取值范围为0≤F≤
| 3 |
答:(1)轻绳可以承受的拉力FT的最大值;
?(2)外力F与tanθ的关系图象如图所示.
点评:本题考查运用数学求极值的方法分析拉力的最大值,由平衡条件得到拉力的函数解析式是关键.

练习册系列答案
相关题目
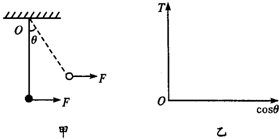 (2006?惠州一模)如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球A,球处于静止状态.现对球施加一个方向向右的外力F,使球缓慢偏移,在移动中的每一刻,都可以认为球处于平衡状态.如果外力F方向始终水平,最大值为2G,试分析
(2006?惠州一模)如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球A,球处于静止状态.现对球施加一个方向向右的外力F,使球缓慢偏移,在移动中的每一刻,都可以认为球处于平衡状态.如果外力F方向始终水平,最大值为2G,试分析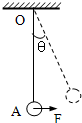 (2008?虹口区二模)如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球A,O点到球心距离为L,开始时球悬垂静止.现对球施加一个方向始终水平向右的力F,使球缓慢偏移,移动过程的每一时刻,都可认为球处于平衡状态.F从开始增大到2G的过程中,轻绳张力T的大小范围为
(2008?虹口区二模)如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球A,O点到球心距离为L,开始时球悬垂静止.现对球施加一个方向始终水平向右的力F,使球缓慢偏移,移动过程的每一时刻,都可认为球处于平衡状态.F从开始增大到2G的过程中,轻绳张力T的大小范围为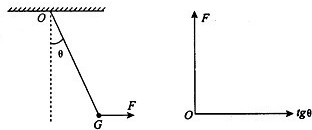 如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球,球处于静止状态,现对球施加一个方向始终保持水平的外力F,使球缓慢地移动,在移动过程中的每一时刻,均可认为球处于平衡状态,如果轻绳可以承受的拉力FT的最大值为2G,设绳与竖直方向夹角为θ求:
如图所示,一根轻绳上端固定在O点,下端拴一个重为G的钢球,球处于静止状态,现对球施加一个方向始终保持水平的外力F,使球缓慢地移动,在移动过程中的每一时刻,均可认为球处于平衡状态,如果轻绳可以承受的拉力FT的最大值为2G,设绳与竖直方向夹角为θ求: