题目内容
（2008?虹口区二模）如图所示，一根轻绳上端固定在O点，下端拴一个重为G的钢球A，O点到球心距离为L，开始时球悬垂静止．现对球施加一个方向始终水平向右的力F，使球缓慢偏移，移动过程的每一时刻，都可认为球处于平衡状态．F从开始增大到2G的过程中，轻绳张力T的大小范围为G≤T≤
G
| 5 |
G≤T≤
G
，此过程中F与T的合力做功大小W=| 5 |
GL（
）
5-
| ||
| 5 |
GL（
）
．5-
| ||
| 5 |
分析：F从开始增大到2G的过程中，轻绳张力T逐渐增大，分析小球的受力，根据平衡条件求解张力的最小值和最大值，即可得到范围．根据动能定理求F与T的合力做功．
解答：解：球悬垂静止时，轻绳的张力最小，最小值为Tmin=G；
设F增大到2G时，轻绳与竖直方向的夹角为α，如图，根据平衡条件得：
轻绳张力的最大值为Tmax=
=
G
故轻绳张力T的大小范围为G≤T≤
G．
则tanα=
=2
由数学知识得 cosα=
F从开始增大到2G的过程中，由动能定理得：
W-GL（1-cosα）=0
则得F与T的合力做功大小为：W=GL（1-cosα）=GL（
）
故答案为：G≤T≤
G，GL（
）
设F增大到2G时，轻绳与竖直方向的夹角为α，如图，根据平衡条件得：
轻绳张力的最大值为Tmax=
| G2+(2G)2 |
| 5 |
故轻绳张力T的大小范围为G≤T≤
| 5 |
则tanα=
| 2G |
| G |
由数学知识得 cosα=
| ||
| 5 |
F从开始增大到2G的过程中，由动能定理得：
W-GL（1-cosα）=0
则得F与T的合力做功大小为：W=GL（1-cosα）=GL（
5-
| ||
| 5 |
故答案为：G≤T≤
| 5 |
5-
| ||
| 5 |
点评：本题是动态平衡问题，运用平衡条件求解张力．由于T和F的合力是变力，故选择动能定理求它们做功．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
（2008?虹口区二模）如图所示是用转动八面镜法测光速的实验示意图，图中S为发光点，T是望远镜，平面镜O与凹面镜B构成了反射系统．八面镜M距反射系统的距离为AB=L（L可长达几十千米），且远大于OB以及S和T到八面镜的距离．现使八面镜转动起来，并缓慢增大其转速，当转动频率（1秒内转过的圈数）达到f0时（可认为是匀速转动），恰能在望远镜中第一次看见发光点S，由此测出光速c．根据题中所测量的物理量得到光速c的表达式正确的是 （ ）
（2008?虹口区二模）如图所示为起重机沿竖直方向提起的过程中重物运动的速度-时间图象，则该过程中起重机的输出功率最接近下图中的（ ）
（2008?虹口区二模）如图所示，一列简谐横波沿x轴负方向传播，振幅A=4cm．在t=0时刻，平衡位置相距5cm的两质点a、b的位移分别是2cm、-2cm，它们的运动方向都沿y轴的负方向，据此可以推断（ ）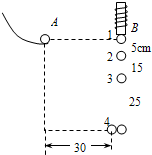
（2008?虹口区二模）如图所示，是利用闪光照相研究平抛运动的示意图，小球A由斜槽滚下，从桌边缘水平抛出，当它恰好离开桌边缘时，小球B也同时下落，闪光频率为10Hz的闪光器拍摄的照片中B球有四个像，像间距离已在图中标出，单位为cm，两球恰在位置4相碰．