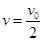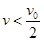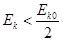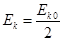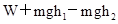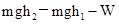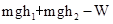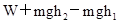题目内容
一个质量为m的物体静止放在光滑水平面上,在互成60°角的大小相等的两个水平恒力作用下,经过一段时间,物体获得的速度为v,在力的方向上获得的速度分别为v1、v2,那么在这段时间内,其中一个力做的功为( )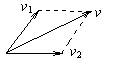
A.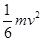 | B.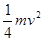 | C.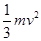 | D.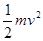 |
B
解析试题分析:据动能定理,合力所做的功等于物体动能的增量,即Fx=mv2/2;两个分力所做的功之和也等于物体动能的增量,即F1x+ F2x= mv2/2,而两个分力大小相等,互成60度角,两个分力在位移方向上的分力大小相等,所以两个分力所做的功相等,即2 F1x="2" F2x= mv2/2,其中一个力作的功就等于mv2/4。B选项正确。
考点:本题考查对动能定理的应用能力。

如图所示,一个带负电的油滴以初速度v0从P点倾斜向上进入水平方向的匀强电场中,若油滴到达最高点C时速度大小仍为v0,则油滴最高点的位置在( )
| A.P点的左上方 | B.P点的右上方 |
| C.P点的正上方 | D.上述情况都可能 |
如图所示,MNP为竖直面内一固定轨道,其1/4圆弧段MN与水平段NP相切于NP端固定一竖直挡板,NP长度为2m,圆弧半径为1m。一个可视为质点的物块自.M端 从静止开始沿轨道下滑,与挡板发生碰撞(只改变速度方向而不改变速度大小)后,最 终停止在水平轨道上某处。已知物块在MN段的摩擦可忽略不计,与NP段轨道间的滑动摩擦因数为0.2。则物块( )
| A.运动过程中与挡板发生2次碰撞 |
| B.返回圆弧轨道的最大髙度为0.6m |
| C.在NP间往返一次克服摩擦力作功8J |
| D.第一与第二次经过圆轨道上N点时对轨道的压力之比为15:7 |
某物体在F的作用下,从光滑斜面的底端运动到顶端,动能的增量为 ,势能的增量为
,势能的增量为 ,则
,则
A.力F所做的功等于 |
B.力F所做的功等于 |
C.合外力所做的功为 |
D.合外力所做功等于 |
如图所示,光滑水平平台上有一个质量为m的物体,地面上的人用跨过定滑轮的绳子向右拉动物体,不计绳和滑轮的质量、滑轮的大小及滑轮的摩擦,人手离滑轮到竖直高度始终为h,所分析的运动过程中,人的初位置在A点,当人以速度v从A匀速运动到B时,人离滑轮的水平距离为x,下列说法正确的是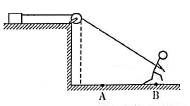
| A.在该运动过程中,物块向右做匀加速运动 |
B.人运动到B位置时,物块的运动速率为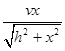 |
C.在该运动过程中,人对物块做的功为 |
D.在该运动过程中,人对物块做的功为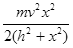 |
如图所示,一个质量为m的物体从高为h的曲面上一点A处,由静止开始下滑,滑到水平面上B点处停止.若再用平行于接触面的力将该物体从B处拉回到原出发点A处,则需要对物体做功的最小值为( )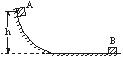
| A.mgh | B.2mgh | C.1.5mgh | D.3mgh |
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力。下列说法正确的是 
| A.小球落地点离O点的水平距离为R |
| B.小球落地点时的动能为5mgR/2 |
| C.小球运动到半圆弧最高点P时向心力恰好为零 |
| D.若将半圆弧轨道上部的1/4圆弧截去,其他条件不变,则小球能达到的最大高度比P点高0.5R |
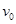 、
、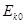 ,小球能达到的最大高度为
,小球能达到的最大高度为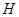 。若运动过程中小球所受的空气阻力大小不变,小球上升到离水平面的高度为
。若运动过程中小球所受的空气阻力大小不变,小球上升到离水平面的高度为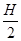 时,小球的速度和动能分别为
时,小球的速度和动能分别为 、
、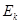 ,则
,则