题目内容
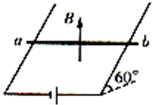如图所示，在与水平方向成60°角的光滑金属导轨间连一电源，在相距lm的平行导轨上放一重为3N的金属棒ab，棒上通过3A的电流，磁场方向竖直向上，这时棒恰好静止，求：（1）匀强磁场的磁感应强度；
（2）ab棒对导轨的压力；
（3）若要使B取值最小，其方向应如何调整？并求出最小值．
分析：（1）根据共点力平衡求出安培力的大小，从而根据F=BIL求出磁感应强度的大小．
（2）根据共点力平衡，运用合成法求出支持力的大小，从而得出对导轨的压力．
（3）当安培力平行斜面向上时，F有最小值，即磁感应强度具有最小值．
（2）根据共点力平衡，运用合成法求出支持力的大小，从而得出对导轨的压力．
（3）当安培力平行斜面向上时，F有最小值，即磁感应强度具有最小值．
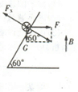
解答：解：（1）棒静止时，受力如图．
则有：F=Gtan60°
即BIL=Gtan60°
解得B=
=
T．
故匀强磁场的磁感应强度大小为
T．
（2）ab棒对导轨的压力与FN大小相等．
FN=
=6N
故ab棒对导轨的压力为6N．
（3）若要使B取值最小，即安培力F最小．显然当F平行斜面向上时，F有最小值，此时B应垂直于斜面向上，且有：
F=Gsin60°
所以BminIL=Gsin60°
Bmin=
=
T．
故当B垂直于斜面向上时，有最小值，为
T．
则有：F=Gtan60°
即BIL=Gtan60°
解得B=
| ||
| IL |
| 3 |
故匀强磁场的磁感应强度大小为
| 3 |
（2）ab棒对导轨的压力与FN大小相等．
FN=
| G |
| cos60° |
故ab棒对导轨的压力为6N．
（3）若要使B取值最小，即安培力F最小．显然当F平行斜面向上时，F有最小值，此时B应垂直于斜面向上，且有：
F=Gsin60°
所以BminIL=Gsin60°
Bmin=
| Gsin60° |
| IL |
| ||
| 2 |
故当B垂直于斜面向上时，有最小值，为
| ||
| 2 |
点评：解决本题的关键会运用合成法处理共点力平衡问题，掌握运用平行四边形定则求出力的最小值．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图所示，在水平地面上放置一块质量为M的长平板B，在平板的上方某一高度处有一质量为m的物块P由静止开始落下．在平板上方附近存在“相互作用”的区域（如图中虚线所示区域），当物块P进入该区域内，B便会对P产生一个竖直向上的恒力F作用，使得P恰好不与B的上表面接触，且F=kmg，其中k=11．在水平方向上P、B之间没有相互作用力．已知平板与地面间的动摩擦因数μ=2.0×10-3，平板和物块的质量之比M/m=10．在P从静止开始下落时，平板B有向左运动的速度v0=0.20m/s，P从静止开始下落到进入相互作用区域经历的时间t0=0.50s．设平板B足够长，保证物块P总能落到B板上方的相互作用区域内，忽略物块P受到的空气阻力，取重力加速度g=10m/s2．求：
（2006?海淀区二模）如图所示，在水平地面上放置一块质量为M的长平板B，在平板的上方某一高度处有一质量为m的物块P由静止开始落下．在平板上方附近存在“相互作用”的区域（如图中虚线所示区域），当物块P进入该区域内，B便会对P产生一个竖直向上的恒力f作用，使得P恰好不与B的上表面接触，且f=kmg，其中k=11．在水平方向上P、B之间没有相互作用力．已知平板与地面间的动摩擦因数μ=2.0×10-3，平板和物块的质量之比M/m=10．在P开始下落时，平板B向右运动的速度v0=1.0m/s，P从开始下落到进入相互作用区域经历的时间t0=2.0s．设平板B足够长，保证物块P总能落到B板上方的相互作用区域内，忽略物块P受到的空气阻力，取重力加速度g=10m/s2．求：
，平板和物块的质量之比M/m＝10。在P开始下落时，平板B向左运动的速度v0＝1.0m/s，P从开始下落到进入相互作用区域经历的时间t0＝2.0s。设平板B足够长，保证物块P总能落到B板上方的相互作用区域内，忽略物块P受到的空气阻力，取重力加速度g＝10m/s2。求：
，平板和物块的质量之比M/m＝10。在P开始下落时，平板B向左运动的速度v0＝1.0m/s，P从开始下落到进入相互作用区域经历的时间t0＝2.0s。设平板B足够长，保证物块P总能落到B板上方的相互作用区域内，忽略物块P受到的空气阻力，取重力加速度g＝10m/s2。求：
，平板和物块的质量之比M/m＝10。在P开始下落时，平板B向左运动的速度v0＝1.0m/s，P从开始下落到进入相互作用区域经历的时间t0＝2.0s。设平板B足够长，保证物块P总能落到B板上方的相互作用区域内，忽略物块P受到的空气阻力，取重力加速度g＝10m/s2。求：