��Ŀ����
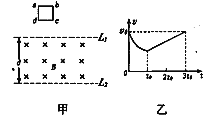
����Ŀ����ͼ��ʾ������Ϊm��������Ϊ+q�Ĵ��������ɾ�ֹ��ʼ����ѹΪU0�ļ��ٵ糡���ٺ���ƽ���ڼ���ķ���ӿ����ϼ����λ������ƫת�糡��������ѹΪU���ϼ��������ɣ����峤�Ⱥͼ������ΪL�����Ӵ���һ�����ƫת�糡��������ڵ���ǿ�ų����Ÿ�Ӧǿ��ΪB���ų�����ֱ��ֽ�����⣬�ų�ֻ������MN�Ҳ��ij���������������ڣ�MNΪ�ų���һ���߽磬���Ե糡�ʹų���ľ��룬���ƴ������ӵ�������
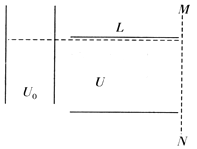
(1)���ӽ���ƫת�糡ʱ���ٶȣ�
(2)��ƫת��ѹU=0ʱ���������������մ�MN�߽��뿪�ų�����ų��������С���S1��
(3)��ƫת��ѹU=2U0ʱ���������������մ�MN�߽��뿪�ų�����ʱ�ų��������С���ΪS2����![]() ��
��
���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
��������(1)���������ڵ糡�м��٣�![]()
��ã�![]() ��
��
(2)����ƫת��ѹU=0����ֱMN����ų����ڴų��������Բ���˶����MN����ų����켣��ͼ��
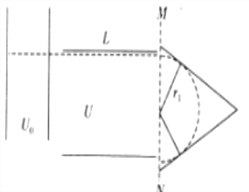
![]()
���������δų�������Ϊb����
![]()
�����Ǵų���������Ϊ![]()
��ã�![]() ��
��
(3)��ƫת��ѹU=2U0ʱ������������ƫת�糡�У��켣��ͼ��
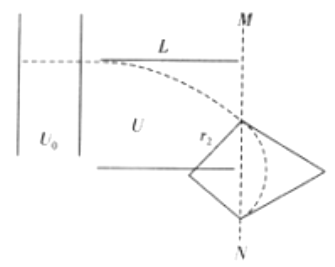
L=v1t
![]()
�뿪ƫת�糡ʱ��ƫת��![]()
��ã�![]()
�����ӽ���ų�ʱ���ٶ�![]()
����������ڴų��е��˶��뾶Ϊr2
![]()
���ʱ�����Ǵų��ı߳�Ϊc
����ݼ��ι�ϵ��![]()
![]()
��ã�![]() ��
��