题目内容
13.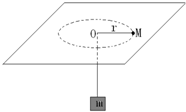 如图所示,细绳一端系着质量M=4kg的物体,静止在水平台面上,另一端通过光滑小孔吊着物体m,M的中心与圆孔距离r=0.5m,已知M与水平面的最大静摩擦力为12N,现使此平面绕中心轴以角速度ω=3rad/s匀速转动,问m的质量满足什么条件可使m会处于静止状态?
如图所示,细绳一端系着质量M=4kg的物体,静止在水平台面上,另一端通过光滑小孔吊着物体m,M的中心与圆孔距离r=0.5m,已知M与水平面的最大静摩擦力为12N,现使此平面绕中心轴以角速度ω=3rad/s匀速转动,问m的质量满足什么条件可使m会处于静止状态?
分析 当m质量最大时,由于细绳的拉力作用,M有向圆心运动趋势,静摩擦力方向和指向圆心方向相反,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力.当m质量最小时,M有离开圆心趋势,静摩擦力方向指向圆心方向,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力.根据牛顿第二定律求解即可.
解答 解:当m质量最大时,M有向圆心运动趋势,故水平面对M的静摩擦力方向和指向圆心方向相反,且等于最大静摩擦力12N.
根据牛顿第二定律隔离M有:
mmaxg-fm=Mω2r
解得:mmax=3kg,
当m质量最小时,M有离开圆心趋势,水平面对M摩擦力方向指向圆心,大小也为2N.
再隔离M有:
mmin+fm=Mω2r
解得:mmin=0.6kg
所以m范围是:0.6kg≤ω≤3kg
答:m的质量满足0.6kg≤ω≤3kg可使m会处于静止状态.
点评 本题考查应用牛顿定律处理临界问题的能力.当物体将滑动时,静摩擦力达到最大值,难度适中.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3. 奥斯特发现了电流周围能产生磁场,法拉第认为磁也一定能生电,并进行了大量的实验.图中环形物体是法拉第使用过的线圈,A、B两线圈绕在同一个铁环上,A与直流电源连接,B与电流表连接.闭合开关后发现电流表指针并不偏转,即没有“磁生电”.其原因是( )
奥斯特发现了电流周围能产生磁场,法拉第认为磁也一定能生电,并进行了大量的实验.图中环形物体是法拉第使用过的线圈,A、B两线圈绕在同一个铁环上,A与直流电源连接,B与电流表连接.闭合开关后发现电流表指针并不偏转,即没有“磁生电”.其原因是( )
 奥斯特发现了电流周围能产生磁场,法拉第认为磁也一定能生电,并进行了大量的实验.图中环形物体是法拉第使用过的线圈,A、B两线圈绕在同一个铁环上,A与直流电源连接,B与电流表连接.闭合开关后发现电流表指针并不偏转,即没有“磁生电”.其原因是( )
奥斯特发现了电流周围能产生磁场,法拉第认为磁也一定能生电,并进行了大量的实验.图中环形物体是法拉第使用过的线圈,A、B两线圈绕在同一个铁环上,A与直流电源连接,B与电流表连接.闭合开关后发现电流表指针并不偏转,即没有“磁生电”.其原因是( )| A. | 线圈A中的电流较小,产生的磁场不够强 | |
| B. | 线圈B中产生的电流太小,电流表指针不偏转 | |
| C. | 线圈A中的电流是恒定电流,不会产生磁场 | |
| D. | 线圈A中的电流是恒定电流,产生稳恒磁场 |
4. 在水平地面上竖直插入一对电极M和N,将两个电极与直流电源相连,大地中形成电场.电场的基本性质与静电场相同,其电场线分布如图所示,P、Q是电场中的两点.下列说法正确的是( )
在水平地面上竖直插入一对电极M和N,将两个电极与直流电源相连,大地中形成电场.电场的基本性质与静电场相同,其电场线分布如图所示,P、Q是电场中的两点.下列说法正确的是( )
 在水平地面上竖直插入一对电极M和N,将两个电极与直流电源相连,大地中形成电场.电场的基本性质与静电场相同,其电场线分布如图所示,P、Q是电场中的两点.下列说法正确的是( )
在水平地面上竖直插入一对电极M和N,将两个电极与直流电源相连,大地中形成电场.电场的基本性质与静电场相同,其电场线分布如图所示,P、Q是电场中的两点.下列说法正确的是( )| A. | P点场强比Q点场强大 | |
| B. | P点电势比Q点电势高 | |
| C. | 电子在P点的电势能比在Q点的电势能大 | |
| D. | 电子沿直线从N到M的过程中所受电场力一直做正功 |
1. 如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
 如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )
如图所示,一个卫星围绕某行星做匀速圆周运动,此行星的质量和半径分别是地球质量M和半径R的a倍和b倍,万有引力常量为G,则下列说法正确的是( )| A. | 卫星在轨道上运动的速度大于第一宇宙速度 | |
| B. | 此行星的第一宇宙的速度是地球第一宇宙的$\sqrt{\frac{a}{b}}$倍 | |
| C. | 卫星轨道上运动时,如果速度减小,卫星将到达高轨道运动 | |
| D. | 如果卫星公转周期等于行星的自转周期,则卫星是该行星的同步卫星 |
8.下面关于丹麦天文学家第谷,对行星的位置进行观察所记录的数据,说法正确的是( )
| A. | 这些数据误差相当大 | |
| B. | 这些数据说明太阳绕地球运动 | |
| C. | 这些数据与以行星绕太阳做匀速圆周运动为模型得到的结果相吻合 | |
| D. | 这些数据与以行星绕太阳做椭圆运动为模型得到的结果相吻合 |
5.某物体运动的v-t图象如图所示,则下列说法正确的是( )


| A. | 物体在第1s末运动方向发生改变 | |
| B. | 物体在第2s内、第3s内的加速度是相同的 | |
| C. | 物体在第2s末离出发点最远,且最大位移为1m | |
| D. | 物体在第5s时离出发点最远,且最大位移为0.5m |
2.某实验小组采用如图甲所示的装置探究功与速度变化的关系.
(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
为进一步直观反映功与速度变化的关系,请根据如表数据,选择恰当的物理量在图丙所示的坐标系中作出相应的图象.
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.

(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
| 数据 项目 次数 | 橡皮筋做的功 | 10个均匀间隔的距离xn(m) | 10个间隔的时间t(s) | 小车获得的速度vn(m/s) | 小车速度的平方vn2(m2/s2) |
| 1 | W | 0.288 | 0.2 | 1.44 | 2.07 |
| 2 | 2W | 0.417 | 0.2 | 2.09 | 4.37 |
| 3 | 3W | 0.489 | 0.2 | 2.45 | 6.00 |
| 4 | 4W | 0.590 | 0.2 | 2.95 | 8.70 |
| 5 | 5W | 0.648 | 0.2 | 3.24 | 10.50 |
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.

 如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r.
如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r.