题目内容
3.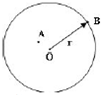 如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r.
如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r.
分析 已知圆盘转动的角速度,则由v=ωr可求得线速度大小;根据向心加速度公式a=ω2r可求得向心加速度.
解答 解:由v=rω可知,A点的线速度为:
v=ω×$\frac{r}{3}$=$\frac{ωr}{3}$;
向心加速度为:
a=ω2r
故答案为:$\frac{ωr}{3}$,ω2r
点评 本题考查线速度与角速度之间的关系及向心加速度的公式应用,一定要注意根据已知条件选择合适的向心加速度公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.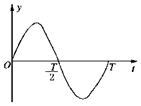 一弹簧振子做简谐运动,其振动图象如图所示,那么在($\frac{T}{2}$-△t)和($\frac{T}{2}$+△t)(△t是极短的时间)两时刻,振子的:
一弹簧振子做简谐运动,其振动图象如图所示,那么在($\frac{T}{2}$-△t)和($\frac{T}{2}$+△t)(△t是极短的时间)两时刻,振子的:
①速度相同;
②加速度相同;
③相对平衡位置的位移相同;
④动的能量相同.
以上选项中正确的是( )
 一弹簧振子做简谐运动,其振动图象如图所示,那么在($\frac{T}{2}$-△t)和($\frac{T}{2}$+△t)(△t是极短的时间)两时刻,振子的:
一弹簧振子做简谐运动,其振动图象如图所示,那么在($\frac{T}{2}$-△t)和($\frac{T}{2}$+△t)(△t是极短的时间)两时刻,振子的:①速度相同;
②加速度相同;
③相对平衡位置的位移相同;
④动的能量相同.
以上选项中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
11.两个分别带有电荷量-Q和+4Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F,两小球相互接触后将其固定距离变为$\frac{1}{2}$r,则两球间库仑力的大小为( )
| A. | 12F | B. | 9F | C. | $\frac{9}{4}$F | D. | F |
18.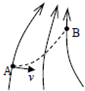 如图所示,实线为电场线的分布情况,某带电粒子仅在电场力作用下由A点运动到B点,虚线为其运动轨迹,粒子在A点的速度方向如图,可以判断( )
如图所示,实线为电场线的分布情况,某带电粒子仅在电场力作用下由A点运动到B点,虚线为其运动轨迹,粒子在A点的速度方向如图,可以判断( )
 如图所示,实线为电场线的分布情况,某带电粒子仅在电场力作用下由A点运动到B点,虚线为其运动轨迹,粒子在A点的速度方向如图,可以判断( )
如图所示,实线为电场线的分布情况,某带电粒子仅在电场力作用下由A点运动到B点,虚线为其运动轨迹,粒子在A点的速度方向如图,可以判断( )| A. | 粒子在A点的加速度大于它在B点的加速度 | |
| B. | 粒子在A点的动能大于它在B点的动能 | |
| C. | 粒子在A点的电势能大于在B点的电势能 | |
| D. | A点的电势低于B点的电势 |
8.下列说法中正确的是( )
| A. | 氢原子从激发态向基态跃迁只能辐射特定频率的光子 | |
| B. | 原子核所含核子单独存在时的总质量小于该原子核的质量 | |
| C. | 一个动量为p的电子对应的物质波波长为hp(h为普朗克常量) | |
| D. | 在研究光电效应实验中所测得的遏制电压与入射光的强度有关 |
15.一轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法正确的( )
| A. | 小球过最高点时,杆所受的弹力不可以为零 | |
| B. | 小球过最高点时最小速度为$\sqrt{gR}$ | |
| C. | 小球过最高点时,杆对球的作用力一定与小球所受重力方向相同 | |
| D. | 小球过最高点时,杆对球的作用力方向可以与小球所受重力方向相反 |
13.下列说法中正确的是( )
| A. | 随着科技的发展,永动机是可以制成的 | |
| B. | 某种形式的能量减少,一定有其他形式的能量增加 | |
| C. | 能量耗散表明,在能量的转化过程中能的总量逐渐减少 | |
| D. | 不用电池、也不用上发条的“全自动”手表,说明能量可以凭空产生的 |
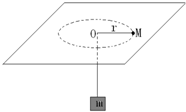 如图所示,细绳一端系着质量M=4kg的物体,静止在水平台面上,另一端通过光滑小孔吊着物体m,M的中心与圆孔距离r=0.5m,已知M与水平面的最大静摩擦力为12N,现使此平面绕中心轴以角速度ω=3rad/s匀速转动,问m的质量满足什么条件可使m会处于静止状态?
如图所示,细绳一端系着质量M=4kg的物体,静止在水平台面上,另一端通过光滑小孔吊着物体m,M的中心与圆孔距离r=0.5m,已知M与水平面的最大静摩擦力为12N,现使此平面绕中心轴以角速度ω=3rad/s匀速转动,问m的质量满足什么条件可使m会处于静止状态? A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则:
A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则: