题目内容
如图所示，光滑绝缘细杆竖直放置，它与正电荷Q为圆心的某圆交于B,C两点，质量为m，带电荷量为-q的有孔小球从杆上A点无初速度下滑，已知q远小于Q，AB=h，BC=3h，小球滑到B点时速度大小为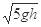
，则：（1）小球到C时的速度大小为___ __；（2）A、C两点电势差___ __。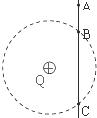
（1）
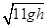（2）
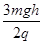
解析试题分析：：(1)因为杆是光滑的，所以小球从A到B过程中只有两个力做功：电场力的功WAB和重力的功mgh，由动能定理得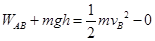
,代入已知条件得电场力做功
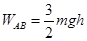,又因为Q为点电荷，B,C为距圆心相等的两点，所以B、C在同一等势面上所以φB=φC，即UAB=UAC，则
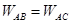,小球从A到C过程中也只有两个力做功：电场力的功WAC和重力的功4mgh，由动能定理
解得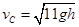
。
(2)因为B、C在同一个等势面上，所以φB=φC，即UAB=UAC由WAB=qUAB=qUAC得,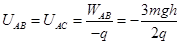
故A、C两点电势差为。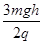
考点：电势差 等势面 动能定理
练习册系列答案
相关题目
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P，然后落回水平面．不计一切阻力。下列说法正确的是 
| A．小球落地点离O点的水平距离为R |
| B．小球落地点时的动能为5mgR/2 |
| C．小球运动到半圆弧最高点P时向心力恰好为零 |
| D．若将半圆弧轨道上部的1/4圆弧截去，其他条件不变，则小球能达到的最大高度比P点高0.5R |
、
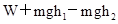
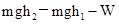
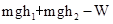
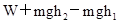
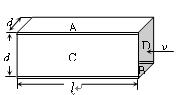
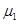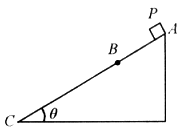
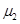。已知P由静止开始从A点释放，恰好能滑动到C点而停下，则
＝_______。
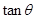kx2其中k为弹簧的劲度系数，x为弹簧的形变量。（g取10 m/s2）。求：
